第六章 美國有多少非裔職業運動員? (Common Nonsenses)
蒙提霍爾問題/一個名叫佛羅里達的女孩/條件機率的混淆/假陽性問題/罕見病問題/達特茅斯鮭魚研究
法國著名的天文學家和數學家 Pierre-Simon Laplace (1749/3/23-1827/3/5) 曾說:「機率只不過是以計算形式呈現的常識而已。」我們應當對缺乏思考的計算保持警惕。自從電腦問世,計算是一件相當容易的工作,重點是這樣的計算是否有道理。
Monty Hall problem:在電視節目 Let’s Make a Deal (我們來做個交易吧) 中,參賽者經常得在三扇門間選一個。對於這種情況,有個統計決策能幫助你贏得 Buick 汽車,而非一輩子供應的 Rice-A-Roni 食品。

|
門後是汽車的初始機率 (在初始狀態,你失敗機率有 ⅔ ) |
door1  | door2  | door3  |
33.33% | 33.33% | 33.33% |
重新描述開始時車子位置的機率 (車子仍 33%、非車子為 66%) |
door1  | door2  | door3  |
33.33% | 66.66% |
假設主持人打開 door 2,不是贏家的機率變成如下 |
door1  | door2  | door3  |
33.33% | 0% | 66.66% |
|
三種可能的情況,假設你都猜 Door 1,主持人翻開第一扇門都不是汽車 |
🚪 Door 1 |
🚪 Door 2 |
🚪 Door 3 | 主持人開第幾扇門 | 當開第一扇門,發現不是汽車後的決定 | 不換 | 換 | 🚗 | 🍲 | 🍲 | 1 | 🚗 (直接猜中) | 🍲 | 🍲 | 🚗 | 🍲 | 3 | 🍲 | 🚗 | 🍲 | 🍲 | 🚗 | 2 | 🍲 | 🚗 |
Ref: https://brilliant.org/wiki/monty-hall-problem/ |
Bayes Theorem |
公式:P(Ak | B)=P(B | Ak) P(Ak)iP(B | Ai) P(Ai) 初始狀態,每扇門後是汽車的機率:P(D1)=P(D2)=P(D3)=13 假設你先選 Door1 ,主持人打開 Door3,發現門後不是汽車,機率變成:P(car | D1)=12、P(car | D2)=1、P(car | D3)=0 分母:P(car | D1) P(D1)+P(car | D2) P(D2)+P(car | D3) P(D3)=1213+113+013=16+13=36=12 堅持 Doo1 不換門,獲得汽車的機率:P(D1 | car)=P(D1) P (car | D1)P(car | D1)P(D1)+P(car | D2)P(D2)+P(car | D3)P(D3)=131212=13 換 Door3,獲得汽車的機率:P(D2 | car)=P(D2) P (car | D2)P(car | D1)P(D1)+P(car | D2)P(D2)+P(car | D3)P(D3)=13112=23
Ref: https://www3.nd.edu/~jstiver/Exec_Micro/Monty%20Hall.pdf |
我們看到黑人在職業運動佔有很高比例,因此下意識覺得很大一部分黑人都是職業運動員。如果將話題從種族變成性別,這錯誤將更明顯。NBA 所有球員都是男性,但在 NBA 打籃球的男性占美國男性群體比例很少。許多非裔美國孩子希望成為下一位 Michael Jordan、Magic Johnson、Lebron James、Kevin Durant,遺憾的是,他們幾乎無法成功。這是條件機率的混淆,擁有夢想與抱負很好,但認清現實更重要。學術與體育都很重要,兩者皆應當受到尊重,兩者相比,從事學術更有可能得到一份好工作。
【假陽性問題】假設大麻檢測率有 95% 的檢驗準確率、估計 5% 的人有吸食大麻,被檢驗出陽性且真的有吸食大麻的人,機率有多高
樹狀圖 |

|
Bayes Theorem 計算過程 |
|
假陽性問題也出現疾病檢測中,和大麻檢測類似,即使疾病檢測有很高的準確率,得到陽性檢測的患者,仍很有可能沒有罹患該疾病。
歷史資料 |

|
樹狀圖 |

|
Bayes Theorem 計算過程 |
|
在醫學上,偽陽性是可被接受的,盡早發現、盡早治療 |

|
假陽性 (false positive) 問題與條件機率的混淆有關。在某些情況,一項檢測很有可能顯示陽性結果,但陽性檢測結果並不能認定疾病的存在,通常還要做更進一步的檢查來做再次確認。對於罕見疾病來說,假陽性會更常見。
醫療檢驗提供診斷用的篩選資訊,但病人經常會理解錯誤,有時甚至醫生也會。了解稱作「敏感度 (sensitivity)」和「特異性 (specificity)」的機率特徵能提供更為準確且 (有的時候) 令人安心的畫面。(Ref: Statistics Hacks: Tips & Tools for Measuring the World and Beating the Odds)
可能的醫療檢驗結果 |
| 病人實際有該症狀 (A) | 病人實際無該症狀 (B) |
檢驗結果顯示有該症狀 | true positive 真陽性 敏感度 (sensitivity) | false positive 偽陽性 |
檢驗結果顯示無該症狀 | false negative 偽陰性 | true negative 真陰性 特異性 (specificity) |
敏感度 (sensitivity) | 特異性 (specificity) |
若一個人真的有該疾病,檢驗結果為陽性的機率有多高 即 A 欄中,有多少比率會得到陽性的檢驗結果
| 若一個人沒有該疾病,檢驗結果為陰性的機率有多高 即 B 欄中,有多少比率會得到陰性的檢驗結果
|
如果一個人得到陽性的檢驗結果,那麼這個人真的有該種疾病的可能性有多高?從病人的角度來看,可被視為這些檢驗基本的有效性考量。病人會問,醫生,我可以相信這些檢驗結果嗎?有可能哪裡出錯嗎? |
10,000 名女性乳房攝影結果 (base rate = 12%, 敏感度約 90%, 特異性約 92%) |
| 病人實際有乳癌 (A) N = 120 | 病人實際無乳癌 (B) N = 9,880 |
乳房攝影指出有癌變 | 真陽性 敏感度 90%N=.9120=108 | 偽陽性 8%N=.089,880=790
|
乳房攝影指出無癌變 | 偽陰性 10%N=.1 120=12
| 真陰性 特異性 (specificity) 92%N=.929,880=9,090 |
A 欄與 B 欄必定是獨立的,各自加起來為 100%,因此能估算偽陰性與偽陽性的比率 898 名拿到陽性結果的女性,有 790 名是錯的,只有 108 名是正確的,因此乳房攝影結果為陽性的受驗者,後續的追蹤檢查最常見的結果實際上是沒有癌症的。較敏感的檢查通常會產生更多的偽陽性,但在生死之間的嚴重狀況中,似乎是我們可接受的代價。 9120 名陰性結果的女性中,有 12 名真的有癌症,因此錯過治療

|
Bayes 的條件機率方法,是「如果這樣,那麼...發生的機率會是怎樣?」是一種條件機率問題,Bayes 的條件機率是檢視事件發生的自然發生頻率。估計在一個人拿到陽性結果的條件像,那個人擁有某種疾病機率的基本公式是:true positivestrue positives + false positives。假設 base rate = .012、seneitivity = .90、specificity = .92,以條件機率表達,公式為 base rate sensitivity(base rate sensitivity)+(1-base rate)(1-specificity)=.012.90(.012.90)+(1-.012)(1-.92)=.1202,代表若一名女性拿到陽性的檢查結果,真的有乳癌的可能性為 12.02%。 |
檢驗報告面面觀:檢驗醫學是臨床醫師在疾病篩檢、診斷與治療與追蹤的重要參考依據,而隨著醫療技術的進步,雖然不斷有推陳出新的新儀器與方法,但每種檢驗方法的敏感性(sensitivity)與特異性(specificity)都不同,且會依使用的檢驗試劑廠牌有差異性,因此在使用新方法前,檢驗室會先進行驗證評估,選擇適當檢驗試劑將差異降低,而不會造成醫師在臨床參考上的困擾。
檢驗特性 | 說明 |
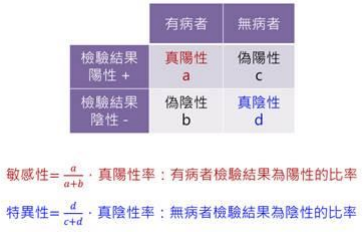
敏感性(sensitivity) | 高敏感性的檢驗,偽陰性率低,因此結果陰性時越能排除得病。 |
特異性(specificity) | 高特異性的檢驗,偽陽性率低,因此結果陽性時越能確認得病。 |
|
No comments:
Post a Comment