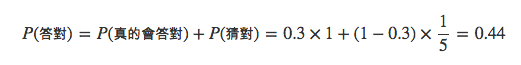[統計] 運用主觀機率 (Subjective Probability) 與貝氏法則 (Bayes’ rule) 來協助做決策

假設有 20 個分析師，面對六個議題的可信度爭論不休，無法得到共識，此時你可以利用主觀概率（Subjective Probability），讓這 20 個專家，針對這六個議題的可信度做出量化的數字，最終並針對每個議題算出標準差，標準差越大，代表意見越分歧。以下圖為例，議題 1 的意見大家較為一致，議題 3 則是意見最分歧

假設日後有新事證出現時，原先的判斷可能會有所調整，此時會採用貝氏法則 (Bayes’ rule)

以議題 1 為例
* 原本評估為真的機率為 P(S1)
* 若為假的機率 P(~S1) = 1 - P(S1)
* P(E|S1) 是當新事證出現時，S1 為真的機率
* P(E|~S1) 是新事證出現時，S1 為假的機率 = 1 - P(E|S1)
* P(S1|E) = P(S1) * P(E|S1) / (P(S1) * P(E|S1) + P(~S1) * P(E|~S1))
經過調整後，會發現標準差微幅增加，代表專家們的意見沒有像之前這麼一致

[統計] 貝氏定理 - Lizard Flu : P(有得病且陰性)

假設有無得病，檢測為陽性的機率分別如下：

假設得病 base rate 為 9%，1000 個人中，有得病與沒得病的人數，且檢測為陰性、陽性的人數分別如下：

計算公式如下：

[統計] 貝氏定理 - Lizard Flu : P(有得病且為陽性)

假設有無得病、檢測為陽性的機率如下：

假設得病 base rate 是 1%，所以 1000 人中，有得病與沒得病人數，且檢測為陰性與陽性的人數分別如下：

計算公式如下

完全訊息期望價值 (EVPI) 的計算

題目

解答
分別計算公寓、辦公大樓與透天厝的預期收益，並取最大值，也就是公寓的預期收益

完全訊息收益就是在每個可能的經濟環境，取最大值並乘以機率

求得完全訊息期望價值

決策樹

[統計] 貝式定理練習2

Reference
[1] 題目來源: https://www.learnmode.net/upload/flip/book/12/129df32e678ac3af/d0469f5495a9.pdf

[統計] 貝式定理練習1

Reference
[1] 題目來源：https://www.learnmode.net/upload/flip/book/12/129df32e678ac3af/d0469f5495a9.pdf