【Hack #41】Play Smart When You Play the Lottery (聰明玩樂透):你贏得大型樂透彩的機率非常非常小,這是事實。與沒有買過其它這本書的樂透玩家相比,這裡可以為你帶來一點優勢,雖然很小。以台灣大樂透為例:
台灣大樂透規則 |
您必須從 01~49 中任選 6 個號碼進行投注。開獎時,開獎單位將隨機開出六個號碼加一個特別號,這一組號碼就是該期大樂透的中獎號碼,也稱為「獎號」。 |
頭獎的可能結果集 |
49484746454443=432,938,943,360 |
頭獎的中獎機率 |
749648547446345244143=5040432,938,943,360=185,900,584
只要累計獎金超過 85,900,584,你就該買! 從統計學的角度來看,只要報償金額超過這個數字,就會是個好賭注。 |
如何避免平分獎金 |
用電腦選號:所有贏錢的彩券中,有 70% 是電腦選號的; 不要用日期選號:如果你要自己選號,避開低於 32 的數字。因為如果你的中獎號碼是別人的幸運日期,就會增加你平分獎金的機會。 遠離眾所皆知的號碼:不要挑選大家都知道的數字,例如 2005 年 10 月的 Powerball 大獎中,有數以萬計的玩家挑選虛構電視劇 Lost 劇情中扮演重要角色的樂透彩券號碼。
|
【Hack #42】Play with Cards and Get Lucky (牌卡幸運玩):
賭你拿到小同花 |
【規則】拿到四張牌的當中,有兩張相同花色的牌 假設已經發了一張牌: 第二張牌與第一張相同花色的機率:(13-1)(52-1)=1251=.2352 第二張牌與第一張不同花色的機率:1-.2352=.7648 第三張牌與頭兩張花色都不同的機率:兩種花色的牌數剩下牌數=13252-2=2650=.52 第四張牌與前三張花色都不同的機率:一種花色的牌數剩下的牌數=1352-3=1349=.2653 四張花色都不相同的機率 = .7648.52.2653=.1055,拿到小同花的勝率接近九成
|
用兩副紙牌找到相同的牌 |
【規則】假設兩副紙牌,同時發出相同的牌 (例如 8♣),你就算贏 假設已經從一副紙牌抽出一張: |
【Hack #43】Play with Dice and Get Lucky (骰出好運):
兩顆骰子的可能結果、組成與出現機率 |
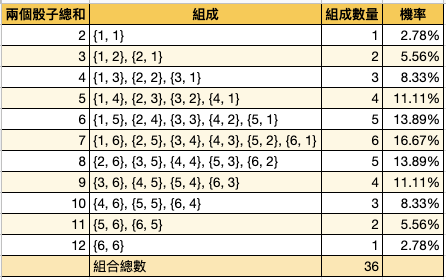
|
請注意,A 欄與 B 欄出現的機率是相等的 |
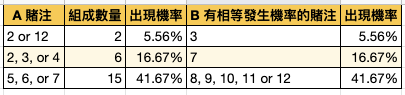
|
假設面臨 A、B 兩種賭注情形,獲勝機率如下 |

|
【Hack #44】Sharpen Your Card-Sharping (磨練你的老千技巧):在德州撲克或其他撲克遊戲中。有幾個基本的初步技能和有關機率的一點基本知識,可以讓你從絕對的初學者變為足以惹上麻煩的老千 (card sharp)。職業玩家比我們更精通撲克牌領域的原因:① 知道在不同階段中,手上的牌碰到想要的牌的粗略機率;② 快速識別其他玩家可能持有較佳牌組的機率。
基礎概念 |
在德州撲克中,你有一半的時間會拿到一對 (pair) 或更好的牌型。 |
機率 |
剩餘可發的牌 | 六張助勝牌 | 三張助勝牌 | 兩張助勝牌 | 5 (翻牌前) | 49% | 28% | 19% | 2 (翻牌後) | 24% | 12% | 8% | 1 (翻牌後) | 13% | 7% | 4% |
如果公用牌沒有... | 你的對手不可能有... | 一對 | 四條 (four of a kind) | 一對 | 葫蘆 (full house) | 同花色的三張牌 | 桐花 | 五張牌範圍內的三張牌 | 順子 |
|
【Hack #45】Amaze Your 23 Closest Friends (讓你最親近的 23 個朋友大吃一驚):一群人中,至少有兩個人生日相同機率有多高?雖然還要視人數多少而定,但這機率卻出乎意料地高。只要人數在 23 人以上,就有高於 50% 的機率。
假設 |
假設生日在人口中是均勻分布相同的 (uniformly distributed),表示一年中每一天出生的人數大致相同。 雖然有四年一次的閏年發生,但是 2/29 出生的人很少,可忽略。
|
全機率法則 (Law of Total Probability) |
此問題有兩個互斥 (mutually exclusive) 的可能結果: ① 至少有兩個人的生日相同 ② 沒有人的生日相同
有時候,判斷一件事情不發生的機率,會比較容易。 你可以發現,當群組大小增加越多,相同生日的機率快速上升: 假設只有兩個人,兩位生日都不相同的機率是:364365=0.997,相同機率 = 1-0.997=0.003 人數增加到三人,不相同機率:364365363365=0.992,相同機率=1-0.992=0.008 (機率增加 2.7 倍) 人數增加到 10 人,不相同機率=364365363365362365361365360365359365358365357365356365355365=0.883,相同機率 = 1-0.883=0.117 (機率增加 39 倍) 人數增加到 23 個人,不相同機率是 0.462,相同機率高達 0.538 (你的勝率大概一半) 人數增加到 30 個人,不相同機率是 0.3,相同機率高達 0.7 (你的勝率高達七成!) 人數增加到 50 個人,不相同機率是 0.03,相同機率高達 0.97 (你的勝率高達 97%!)
|
【Hack #46】Design Your Own Bar Bet (設計你自己的酒吧賭注):做些計算或是使用 spreadsheet software,你就能找出各種「自發性」友善賭注。
原則一 |
計算一個事件跨越多次機會的發生機率的實際公式所依據的概念是,找出一個事件不會發生的比例,然後為每次額外的「擲骰子」把這個比例成以自身,用 1.0 減去結果,就能得到這個事件會發生的機率。
舉例來說,我跟其他兩個人生日月份相同的機率有多少? |
原則二 |
要讓某個人接受賭注,或讓觀眾對任何給定的結果發生感到驚訝,其可能性要讓觀眾感覺必須很小,例如,一群人生日相同的機率。 在單次機會中,不可能發生的機率的確很小,不過,如果你有多次機會,該事件發生的機率就會增加,而且斜率很陡。 |
【Hack #47】Go Crazy with Wild Cards (利用外卡瘋一回):外卡 (wild cards) 被加到撲克牌遊戲中,是為了提升樂趣。不過對統計來說,它讓事情變更讓人困惑。wild cards 通常是小丑牌 (joker),它可以變為持有者希望的任何值。
撲克牌牌型、機率與比較 |
牌型 | 機率 | 相對稀有性 |
同花順 (straight flush) 10♠ J♠ Q♠ K♠ A♠ | .000015 | 可能性低了 16 倍 (.00024.000015=16) |
四條 (four of a kind) 4♠ 4♥ 4♣ 4♦ 9♥ | .000240 | 可能性低了 5.8 倍 (.0014.00024=5.8) |
葫蘆 (full house) 8♠ 8♣ 8♦ K♠ K♥ | .001400 | 可能性低了 1.4 倍 (.0019.0014=1.4) |
同花 (flush) 3♠ 4♠ 8♠ J♠ K♠ | .001900 | 可能性低了 2.1 倍 (.0039.0019=2.1) |
順子 (straight) A♣ 2♣ 3♥ 4♦ 5♠ | .003900 | 可能性低了 5.4 倍 (.021.0039=5.4) |
三條 (three of a kind) 7♠ 7♥ 7♦ 2♣ K♦ | .021000 | 可能性低了 2.3 倍 (.048.021=2.3) |
兩對 (two pair) 8♠ 8♦ A♥ A♣ Q♠ | .048000 | 可能性低了 8.8 倍 (.42.048=8.8) |
一對 (one pair) 9♠ 9♥ 4♣ J♠ A♥ | .420000 | 可能性低了 1.2 倍 (.5.42=1.2) |
什麼都沒有 3♠ 6♥ 9♦ K♠ A♣ | .500000 | --- |
【注意】 玩家有一半的時候,什麼好牌都拿不到。 幾乎有一半的時間會拿到 one pair。 只有 8% (1-.5-.42=.08) 的機率會拿到比 one pair 還好的牌。 同花 (flush) 與葫蘆 (full house) 的機率差不多。 什麼都沒有+one pair = 92% (.5+.42)。 兩對+三條=7%,比三條還好的牌的機率 < 1%。
|
一副牌中有一張外卡的撲克牌組的機率 |
牌型 | 有外卡機率 | 傳統機率 | 有外卡的機率變化 |
五條 (Five of a kind) | .0000045 | --- | --- |
同花順 (straight flush) | .0000640 | .000015 | .000064-.000015.000015100=326% |
四條 (four of a kind) | .0011000 | .000240 | .0011-.00024.00024100=358% |
葫蘆 (full house) | .0023000 | .001400 | .0023-.0014.0014100=64% |
同花 (flush) | .0027000 | .001900 | .0027-.0019.0019100=42% |
順子 (straight) | .0072000 | .003900 | .0072-.0039.0039100=85% |
三條 (three of a kind) | .0480000 | .021000 | .048-.021.021100=129% |
兩對 (two pair) | .0430000 | .048000 | .043-.048.048100=-10% |
一對 (one pair) | .4400000 | .420000 | .44-.42.42100=5% |
什麼都沒有 | .4500000 | .500000 | .45-.5.5100=-10% |
【注意】有 wild cards |
【Hack #48】Never Trust an Honest Coin (永遠不要信任公正的硬幣):人頭 (heads) 或數字 (tails) 的機率各是 50%,對吧?令人不安的答案卻是,並非如此。如果你旋轉 (spin) 一個硬幣,特別是全新的硬幣,數字 (tails) 朝上的情況會比人頭 (heads) 朝上更常見,因為新的硬幣在數字那邊會壓印的比人頭那邊稍微深一點,故人頭那面會稍重。當你要做出瘋狂賭注前,記住,你必須旋轉 (spin) 硬幣,不要翻轉 (flip) 硬幣。
【Hack #49】Know Your Limit (知道你的極限):人類並不總是會做出理性決策,即使是聰明的賭徒,有時候也會拒絕預期報償很大且勝算不錯的賭注。St. Peterburg Paradox (聖彼得堡悖論) 就是健康狀態完全的統計學家大概都不會玩的一種完全公正的賭博遊戲,原因單純是他們剛好是人類。
St. Peterburg 賭注規則 |
你必須支付一個費用給我才能玩。 翻轉一個硬幣,如果人頭朝上,就算你贏,而我會付你 $2。 如果不是人頭,我們就再翻一次。如果這次出現人頭,我會付你 $4 (22)。 假設人頭一直沒出現,我們就再丟一次。假設第三次翻轉出現人頭,我會付你 $8 (23)。
|
硬幣翻轉六次人頭的報償 |
人頭次數 | 可能性 | 贏得賭注 | 預期報償 (expected payoff) |
1 | 12=.5 | 2 | 2+02=1 |
2 | (12)2=14=.25 | 22=4 | 2+02=1 |
3 | (12)3=18=.125 | 23=8 | 2+02=1 |
4 | (12)4=116=.0625 | 24=16 | 2+02=1 |
5 | (12)5=132=.03125 | 25=32 | 2+02=1 |
6 | (12)6=164=.015625 | 26=64 | 2+02=1 |
預期報償 (expected payoff) 是就所有可能結果而言,你平均會贏的金額,例如,贏的時候得 $2,輸的時候得 $0,平均是 $1。 如果你玩這遊戲 64 次,你只有一次會連續出現六次人頭,但你會贏得 $64 你可能擲一次遊戲便結束,也可能反覆擲沒完沒了。問題是,你最多肯付多少錢參加這個遊戲?這個遊戲的期望值是無限大,即你最多肯付出無限的金錢去參加這個遊戲。但是,你更可能只賺到1元,或者2元,或者4元等,而不可能賺到無限的金錢。那你為什麼肯付出無限的金錢參加遊戲呢? 如果限定最多可以擲100次(100次都是反面就沒有錢了),則期望值為50元,但是你應該不會真的付50元去參加這個遊戲。 一局遊戲可能拋一次硬幣就完成,也可能拋100次才完成,其實不難算出平均是2次。於是我們假設平均一秒鐘能完成一局遊戲。如果從宇宙誕生那一刻開始玩這個遊戲玩到現在,玩了138億年,根據前面模擬得到的近似公式,我們可以得出平均收益為:
(log(138e8 * 365 * 24 * 3600) + 2) / log(2) / 2 = 30.7(元) |
【Hack #50】Avoid the Zonk (選對門,避開 Zonk):在電視節目 Let’s Make a Deal (我們來做個交易吧) 中,參賽者經常得在三個簾子間選一個。對於這種情況,有個統計決策能幫助你贏得 Buick 汽車,而非一輩子供應的 Roce-A-Roni 食品。

|
門後是汽車的初始機率 |
door1  | door2  | door3  |
33.33% | 33.33% | 33.33% |
|
重新描述開始時車子位置的機率 (車子仍 33%、非車子為 66%) |
door1  | door2  | door3  |
33.33% | 66.66% |
假設主持人打開 door 2,不是贏家的機率變成如下 |
door1  | door2  | door3  |
33.33% | 0% | 66.66% |
|
【Hack #51】Pass Go, Collect $200, Win the Game (穿越 Go、收取$200、贏得大富翁遊戲):大富翁 (Monopoly) 是機遇的遊戲。因此,贏得勝利最佳策略要以機率為基礎。
骰子機率 |
大富翁是透過兩個骰子的點數,決定你落在哪個方格的主要因素 
|
大富翁獲勝關鍵 |
|
Atlantic City 最佳物業 |

長期坐牢的人:有 12% 的時間,你的對手會落入 Jail 方格。擁有並開發最近假釋的人最有可能落腳的地方,是一個明智目標。這裡指的就是橘色物業,以及雖然沒那麼好但也不錯的紅色物業和紫色物業。不斷被釋放的犯人會湧入盤面的一側,增加在 Illonois 之前的所有物業收租機會。 擁有橘色物業:所有三個橘色物業都在前 10 中。大約每擲 12 次會有一次會碰到,獨佔這些橘色物業並快速發展他們。 避開偏遠之處:也就是綠色物業,綠色物業是玩家較不可能落腳且發展起來最貴的地方。
|
【Hack #52】Use Random Selection as Artificial Intelligence (使用隨機選取作為人工智慧):統計學家早在為處理器問世前,就能建構有智慧的學習型電腦ㄡ你可以使用椰子殼和機率法則來建置會學習井字遊戲 (Tic-Tac-Toe) 永遠不輸的機器。trial-and-error learning process 因具備立即 feedback 的特性,可增加正確選擇的可能性。如果你想要模擬動物的學習方式,你可以調整系統,讓接近遊戲尾聲的動作比在開頭所做的那些有更高的重要性。這是為了反映出一個觀察:時間上越接近行為發生時刻的強化越有效。
【Hack #53】Do Card Tricks Through the Mail (透過郵件來玩紙牌戲法):洗過的一副牌應該要是隨機的,經科學分析顯示,其實並不隨機,而你可以用紙牌分布的已知機率展示驚人的紙牌戲法給素未謀面的人看。
順序 | 洗牌前 | 完美的交錯式洗牌 | 真實世界的交錯式洗牌 |
1 | ♣️ A | ♣️ A | ♣️ A |
2 | ♣️ 2 | ♣️ 7 | ♣️ 7 |
3 | ♣️ 3 | ♣️ 2 | ♣️ 8 |
4 | ♣️ 4 | ♣️ 8 | ♣️ 2 |
5 | ♣️ 5 | ♣️ 3 | ♣️ 3 |
6 | ♣️ 6 | ♣️ 9 | ♣️ 9 |
7 | ♣️ 7 | ♣️ 4 | ♣️ 10 |
8 | ♣️ 8 | ♣️ 10 | ♣️ 5 |
9 | ♣️ 9 | ♣️ 5 | ♣️ 4 |
10 | ♣️ 10 | ♣️ J | ♣️ J |
11 | ♣️ J | ♣️ 6 | ♣️ 6 |
12 | ♣️ Q | ♣️ Q | ♣️ Q |
實現看似不可能的機率 |
猜測次數 | 洗牌兩次 | 洗牌三次 | 洗牌四次 | 洗牌五次 | 洗牌六次 |
1 | 99.7% | 83.9% | 28.8% | 8.8% | 4.2% |
2 | 100% | 94.3% | 47.1% | 16.8% | 8.3% |
3 | 100% | 96.5% | 59.0% | 23.8% | 12.3% |
【Hack #54】Check Your iPod’s Honesty (檢查你的 iPod 是否誠實):找出你 iPod 的隨機 (random) 播放,實際上有多隨機。你的 iPod 假設,如果你沒有為一首歌曲評分,比起你所有指定評分的歌曲 (即使是最低分),你必定更不想常常聽到它。許多人宣稱在 iTunes 隨機播放音樂收藏時,仍可發現某些模式,但那些模式主要是同一位演出者的歌曲被播放多次。如你有 2000 首歌,其中 40 首來自同一歌手,在隨機播放下,有 2% 機率會在下一首聽到他們;接下來 35 首歌中,有 50% 的機率會聽到相同歌手的歌;接下來的50首有 64% 的機率。只要一個低可能性事件 (ex. 2%),只要多幾次發生機會,就會變成高可能性事件 (Hack #46)。
P(n)=1-xtotal-xartistxtotaln, xtotal:總歌曲數, xartist:特定歌手歌曲數
播放次數 | 播放相同歌手的機率 |
1 | 1-100-2100=1-0.98=0.02 |
10 | 1-100-210010=1-0.817=0.183 |
50 | 1-100-210050=1-0.364=0.636 |
100 | 1-100-2100100=1-0.133=0.867 |
【Hack #55】Predict the Game Winners (預測遊戲贏家):相關性 (correlations) 所提供的資訊能讓我們預測任何結果,特別是運動比賽。藉由多元迴歸 (multiple regression) 的技巧,以及電腦軟體的幫忙,可以讓你在遊戲盡情前猜到贏家,訣竅在於挑中正確的預測子 (predictors)。
基礎知識 |
多元迴歸 (multiple regression):用多個變數來預測一個變數,就稱為多元迴歸。挑選正確的預測變數,就會是勝敗關鍵。 |
假設我要預測 Super Bowel 獲勝球隊 |

Y‘=bX1+bX2+bX3+bX4+bX5+a Y‘=.119X1+.000X2+.000X3+.013X4+.001X5+a |
何謂好的「預測子」 |
|
【Hack #56】Predict the Outcome of a Baseball Game (預測棒球比賽的結果):在棒球比賽中途打開廣播聽個五秒鐘,然後關掉。即使沒聽到分數,你也能夠指出誰贏,而且你正確的機率大於一半。
預測原理 |
在棒球中,你作為進攻的一方時間越久,你可能得到的分數就越多。 |
抽樣理論 |
一個樣本最可能被捕捉到的是一個母體最常見的元素。在此,我們的母體就是我們可能聽到的一場比賽的所有瞬間。該母體中,最常見的特性就屬於打擊最多的那一隊。 |
變數挑選 |
真實世界的研究人員經常無法取用他們真正想要了解的變數,而我們使用打擊數 (number of at-bats) 而非打擊時間 (time at bat) 就是很好的例子。在此種情況下,必須接受次佳的可用選擇。科學家將這種取代情況稱為 proxy (委託) 變數或 surrogate (代理) 變數。 |
以 MBL 實驗 |
作者用 Chicago Cubs 這支隊伍做例子,挑選 2003 年的前 25 場,經分析,打擊次數最多得隊伍有 56% 是贏球的;若剔除打擊數一樣的情況,預測就有 63% 的精準度。 |
以 CBPL 2020 年統一與兄弟冠軍戰為例 |
經過七場比賽,最終統一獲得總冠軍。以打擊數做預測,有57%的精準度。 
|
【Hack #57】Plot Histograms in Excel (在 Excel 中繪製直方圖):使用 Microsoft Excel 來繪製資料的分布,可以讓你對統計資訊有更好的理解。直方圖 (histogram) 是了解表現值分布 (distribution of values) 的圖形。
【範例】學生考試分數的分布狀況,假設班級學生的考試分數如下 |
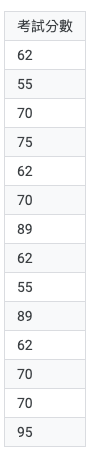
|
以 Google Sheet 操作為例 |
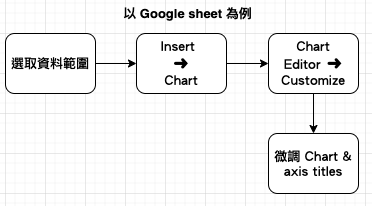
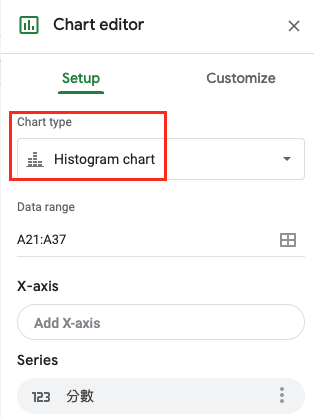
|
執行結果 |

|
【Hack #58】Go for Two (美式足球的兩分轉換):在美式足球中,什麼時候兩分轉換 (two-point coversion) 的嘗試是正確的選擇呢?不管你用的什麼 chart,統計學家加入爭論後,問題就會變得更複雜。
美式足球規則說明 |

|
兩分轉換( two-point conversion) 說明 |
在美式足球中,達陣得分後(達陣本身值 6 分),拿分的隊伍有兩種選項可以得到「額外」的一分或兩分。通常,隊伍會選擇踢過球門柱來多得一分(就像短距射門),但他們也可選擇「多拿兩分」(go for two, 稱為兩分轉換),其中涉及利用跑陣或傳球的進攻方式,嘗試再次得分。
在美式足球和加拿大式足球中,兩分轉換( two-point conversion) 是在達陣得分後可選的兩種追加得分方式之一。此得分方式為在距離達陣區很近的地方按照正常進攻方式嘗試達陣,達陣成功即可在原有達陣 6 分的基礎上再加 2 分,即此次進攻共得 8 分。在不同的規則中,兩分轉換開始進攻的位置是不同的,從5碼線到2碼線不等。
根據歷史資料顯示,平均 NFL 足球隊大約有 98% 能拿到額外一分,而嘗試兩分時,大約有 40% 成功機率。
教練會額外因素納入考量: |
運作方式 (適用於第四節決勝關鍵) |
假設 50% 的延長賽獲勝機率 你有 98% 踢出一個加分球,並有 50% 的機率贏得延長賽,那麼那額外一分有 49% 的獲勝機率(.98.50=.49)。 你有 40% 達成兩分轉換,所以要那兩分會讓你有 40% 勝利機會。失敗就比賽結束,而成功就贏得比賽。 49% 比 40% 還要好,所以你該選擇拿額外一分就好。請注意,如果你相信你球隊達成兩分轉換的機率 > 49%,就該去嘗試。
|
【Hack #59】Rank with the Best of Them (躋身最佳選手之列):有許多方式可以使用資料來判斷在任何運動中,誰是最佳選手。然後,在個別運動中,比較表現的所有直覺方法都有有效性的疑慮。
夏季撲克聯盟參賽者與所獲得點數 |

|
用三種評估指標來總結每個參賽者的表現 |
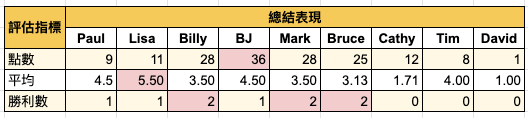
|
三種評估指標卻得到不同的排名結果 |
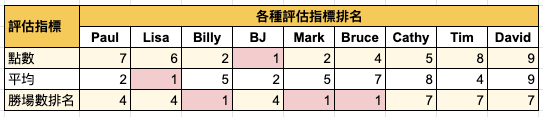
|
本 Hack 目的 |
|
【Hack #60】Estimate Pi by Chance (以機率估算圓周率):統計學家很喜歡認為任何重要的事都可透過統計學來發現。實際上可能是真的,因為我們發現,你甚至可以使用統計學來估計科學中最重要的基本數值,也就是 pi (圓周率)。
Buffon’s Needle Problem (布豐的掉針問題) |
想像有一根針,隨機落在畫有兩條平行水平線上的圖。這兩條線之間的距離比針的長度還要長。這根針落在其中,並觸碰到其中一條線的機率為何? 
|
計算機率考量的因素 |
任何給定的隨機掉落位置有以下關鍵因素 針的中心位於何處; 針與最接近的直線之垂直線所組成的角度。
透過上述兩個關鍵因素,簡化問題為 若針的中心點剛好落在其中一條線上,無論角度為何,一定有碰到那條線; 若針的中心點足夠接近一條線,在針的長度一半內,有可能會碰到一條線,一切要看其落下角度 若針的中心點與一條線的距離 > 針的長度的一半,不管角度為何,永遠不會碰到線; 落下的位置越接近線,針碰觸到線的機率就越大。
|
計算針落到直線的機率 |
針落下的所有可能位置可被繪製成一條曲線,代表著與一條直線的所有可能距離,以及針與垂直線的所有可能角度。這需要用到三角學 (Trigonometry),而數學家使用方程式來定義這條曲線 (假設針的長度是 3 英吋、兩條直線間的距離為 4 英吋):機率=(2)(針的長度)()(直線間的距離)=(2)(3)(3.1459)(4)=.477,代表有 48% 的機率會碰到一條線。 機率和 𝛑:=(2)(針的長度)(機率)(直線間的距離)=(2)(3)(.477)(4)=3.1447
|
用機率估計 pi |
假設你被困在荒島上,不知道 pi value為何。你可以設置兩條水平線的區域,丟下針,然後記錄結果。測量你的水平線的距離以及針的長度,從多次落下的針,收集大量樣本。假設針有 7 英吋,兩條線間的距離是 8 英吋,經過實驗 1000 次,針碰到線的機率是 55%: =(2)(針的長度)(機率)(直線間的距離))=(2)(7)(.55)(8)=3.18 |
No comments:
Post a Comment