統計感興趣的一直都是變數間的關係 (relationships among variables)。舉例來說,相關係數 (correlation coefficient) 是兩組分數間關係的強度和方向的指數 (index)。測量關係的統計程序的例子包括 t 檢定;以及一次比較兩個以上群組的變異數分析 (analysis of variance)。
三種典型的效應大小類型
effect size type | 說明 |
相關係數 (correlation coefficient) | 相關性 (corrleation) 以符號 r 來代表,是變數間關係的度量,是一種效應大小 由於相關性可能是負值,所以有時會被平方已產生一個永遠 > 0 的值,即 r2 (變異比例, proportion of variance)。
|
d | d=tSample Size in Group 1 + Sample Size in Group 2(Sample Size in Group 1) (Sample Size in Group 2) |
Eta 平方 (Eta-squared) | |
解讀 effect size 多大算大的經驗法則 |
effect size | 小 | 中 | 大 | r | ±.10 | ±.30 | ±.50 | r2 | .01 | .09 | .25 | d | .2 | .5 | .8 | 2 | .01 | .06 | .14 |
|
如何解讀研究發現
解讀研究發現 | 說明 | 例子 |
統計顯著性 (statistically significant) | 回答這個關係可能出現在母體嗎? | 服用 aspirin 的患者,心臟病發的可能性是服用安慰劑哪組的 50%,代表有統計顯著性 |
效應大小 (effect size) | 回答這個關係有多大? | 運用比例式比較 (proportional comparison) 的公式,此研究的 effect size = .06 個標準差,or .06 的 d,代表 aspirin 與心臟病的關係真實存在,但是沒有很強烈 |
顯著性 (significance) 告訴你的是此關聯可能存在於母體中,若是效應很小,使得沒人對它有興趣。 |
【Hack #11】 Discover Relationships (發現關係):只要記錄觀測值並計算神奇又玄妙的相關係數 (correlation coefficient),就能揭露世界中隱藏的關係。統計研究人員會把假設 (assumption) 稱為:關於變數 (variables) 間關係的假說 (hypotheses)。

計算「相關係數」:計算結果只能看出是否有相關性,「不是」因果關係。

受訪者 | 對起司態度 | 對起司蛋糕態度 | 起司的 Z-scores | 起司蛋糕的 Z-Scores | Z-scores 的乘積 |
Larry | 50 | 36 | 1.09 | 1.13 | 1.23 |
Moe | 45 | 35 | 0.77 | 1.00 | 0.76 |
Curly | 30 | 22 | -0.19 | -0.75 | 0.14 |
Shemp | 30 | 25 | -0.19 | -0.35 | 0.07 |
Groucho | 10 | 20 | -1.47 | -1.02 | 1.50 |
平均數 | 33.00 | 27.60 | 相關係數 | 0.93 (ZxZy)N - 1 |
標準差 | 15.65 | 7.44 |
計算結果 | 非常接近 1.0,有強烈正相關 (positive correlation) |
為任何兩個變數間產生相關係數(關係強度的度量值)適用於:
相關係數適用性 | 說明 |
① 數字必須有真正的意義,且代表某種底層的連續概念 | 連續變數 (continuous variable) 包含溫度、薪資等;類別變數 (categorical variable) 包含性別、教育程度、宗教信養、考試名次等。 |
② 變數必須有變動 | 如果每個人對起司的感受都相同,你就無法計算與起司蛋糕或巧克力或其他東西的態度之相關性。 |
③ 具備統計顯著性所需的最小相關性大小 | 如下表所示,而且只有在樣本是隨機從母體抽取的情況下才會精準。 |
很可能不是碰巧發生的相關性 |
Sample Size | 被視為具有統計顯著性的最小相關性 |
5 | .88 |
10 | .63 |
15 | .51 |
20 | .44 |
25 | .40 |
30 | .38 |
60 | .26 |
100 | .20 |
相關係數計算
題目說明 |
某財務軟體公司在全國有許多代理商,為研究它的財務軟體產品的廣告投入與銷售額的關係,統計人員隨機選擇10家代理商進行觀察,搜集到年廣告投入費和月平均銷售額的數據,並編製成相關 (https://reurl.cc/xg6G24) 
|
計算過程 |
excel function:CORREL(年廣告費投入資料, 月均銷售額資料), 例如,CORREL(A2:A11, B2:B11) 相關係數 = 0.9942 相關係數 r = 0.9942 > 0.63,廣告投入費與月平均銷售額之間有高度的線性正相關關係
|
【Hack #12】Graph Relationships (圖形關係):只要兩個變數間的某個關係被發現而且有了定義,我們就能使用其中一個變數來猜測另一個,畫出一條迴歸線 (regression line) 能讓你圖形化這個關係並做出預測。

例如,我們可以產生以下公式來預測華氏氣溫幾度時,會賣出幾份冰淇淋
Cones Sold = 15+(Temperature .50)
regression line 的適用性
【Hack #13】Use One Variable to Predict Another (使用一個變數來預測另一個):simple linear regression 是度量看不見的東西或預測尚未發生的事件結果的強大工具。藉由統計學的幫忙,你就能在只看到另一個變數表現時,準確猜測某人在目標變數上可能的 scores。迴歸分析(Regression Analysis)是利用一組自變數(或稱預測變數、獨立變數、predictor variable)對某一因變數(或稱準則變數、criterion variable)建立關係式以便做為預測的依據,它也可以做為評估自變數對因變數的效用。迴歸的主要目的是做預測,只用一個自變數來預測應變數稱為 simple linear regression;用一個以上的自變數來預測因變數稱為 complex linear regression。
變數 | 變數類型 | 平均數 | 標準差 |
ACT Scores | 自變數 (predictor variable) | 20.10 | 2.38 |
GPA Scores | 因變數 (criterion variable) | 2.98 | 0.68 |
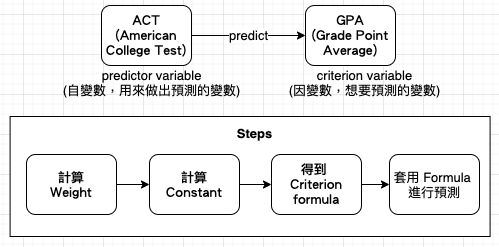
Weight=correlation coefficientCriterion Standard DeviationPredictor Standard Deviation=0.55.682.38=.16
Constant = Criterion Mean-(WeightPredictor Mean)=2.98-(.1620.1)=-.24
Criteria=Constant+(PredictorWeight)
Predict GPA=-.24+(ACT Score.16)
申請人 | ACT Score | Predict GPA |
Melissa | 26 | -.24+(26.16)=3.90 |
Bruce | 14 | -.24+(14.16)=2.00 |
regression analysis 的適用性
regression analysis | 說明 |
適用於 | |
不適用於 | 若兩個變數間的相關性不完美,預測的準確性也不會完美:由於沒有完美的 1.0 相關性存在,你可以用估計的標準差 (standard error of estimate) 來判斷你的誤差大小。 變數的關係強度的分佈不是線性:若變數的關係強度的分佈不是線性,預測就會產生很大的誤差。 收集的資料沒有代表性:若一開始收集來建立迴歸方程式中的那些資料沒有代表性,預測結果也會有錯。
|
【Hack #14】Use More Than One Variable to Predict Another (使用多個變數來預測另一個):統計學家經常會使用一個變數來預測另一個變數,以回答疑問並運用相關性資訊來解決問題。不過為了更精確地預測,可使用多元迴歸 (multiple regression) 將多個預測變數結合到單一個 regression equation 中。multiple regression 較 simple regression 準確,因 mutiple regression 知道每個 predictor 之間的關聯性,並建立更準確的權重。例如,以下從一個預測變數(自變數)變成多個預測變數,每個 predictor 都有自己的權重:
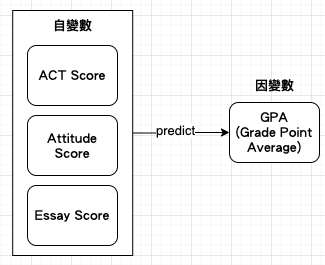
一個自變數:Criteria=Constant+(PredictorWeight)
三個自變數:Criterion=Constant+(Predictor 1 Weight 1)+(Predictor 2 Weight 2)+(Predictor 3 Weight 3)
產生預測 GPA 公式 (權重是虛構,ACT Score 的 .02 權重比 Attitude Score 大,並不是代表前者比後者重要,只是單純是所使用的尺度<scale> 不同。ACT Score 範圍是 1.0 ~ 4.0,Attitude Score 範圍則是 20 ~ 100):Predicted GPA = 3.01 + (ACT Score * .02) + (Attitude Score * .007) + (Essay Score * .025)
標準化權重 (standardized weights) 是將原始資料轉換為 z scores,即每個原始分數與平均值之間的距離以標準差表達,如此一來就能公平比較並被理解。
自變數 | 非標準化權重 | 標準化權重 |
Constant | 3.01 | - |
ACT Score | .02 | .321 |
Attitude Score | .007 | .603 |
Essay Score | .025 | .156 |
【Hack #15】Identify Unexpected Outcomes (識別出未預期的結果):要如何得知觀測是正確的還是有所偏差?要如何知道比起碰巧發生,那多少有背後的原因存在?你可以使用單向卡方檢定 (chi-square test) 來確定這些事。此檢定名稱是因為用於所產生的臨界值 (critical value) 的符號是一個 X,它是希臘字母 chi (唸做「凱」),計算中所需的值都會經過平方運算 (squared),因此稱作 chi-square or chi-squared。
犯罪事件數 |
0:00 ~ 8:00 | 8:00 ~ 16:00 | 16:00 ~ 0:00 | Total |
120 | 90 | 90 | 300 |
【檢測目的】不同時段會發生不同數量的犯罪是件數,這是偶然嗎? |
計算過程 |
Chi-square=(Observed Frequency-Expected Frequency)2Expected Frequency 假設犯罪事件總數 300 件,預期三個時段平均各出現 100 件 (3003): Chi-square=(120-100)2100+(90-100)2100+(90-100)2100=400100+100100+100100=6 |
顯著水平 .05 的關鍵卡方值 |
2 個類別 | 3 個類別 | 4 個類別 | 5 個類別 | 3.84 | 5.99 | 7.82 | 9.49 | |
|
chi-square 適用性 |
適用於類別資料 (categorical data) | | 適用於適合度檢定統計量 (goodness-of-fit statistic) | |
|
【Hack #16】Identify Unexpected Relationships (識別出未預期的關係):如果你想要驗證兩個變數間觀察到的某種關係是否存在,你可以使用雙向卡方檢定 (two-way chisquare test)。這裡有幾個你可能有的假設,隱含著類別變數間的某種關係:學生經常上課心不在焉;電腦程式設計師會玩寶可夢;收集漫畫書的大人會撰寫 Statistics Hacks 這種書。此hack 用來判斷我們持有的某種刻板印象是否正確。
單向 / 雙向卡方檢定 |

|
二者通用的卡方公式 |
Chi-square=(Observed Frequency-Expected Frequency)2Expected Frequency |
假想的選民樣本 |
政黨 | 男性 | 女性 | 總數 | 共和黨 | 45 | 30 | 75 | 民主黨 | 34 | 41 | 75 | 總數 | 79 | 71 | 150 |
|
計算過程 |
政黨 | 男性 | 女性 | 共和黨 | 7579150=39.5 | 7571150=35.5 | 民主黨 | 7579150=39.5 | 7571150=35.5 |
卡方值=(45-39.5)239.5+(34-39.5)239.5+(30-35.5)235.5+(41-35.5)235.5=3.24 |
顯著水平 .05 的關鍵卡方值 |
2 個類別 | 3 個類別 | 4 個類別 | 5 個類別 | 3.84 | 5.99 | 7.82 | 9.49 | |
|
【Hack #17】Compare Two Groups (比較兩個群組):哪個比較好?誰擁有比較多?人與人之間真有差異嗎?如果你想要為你的這些關於最好、最多或最少的信念找出一些真實的證據,你可以使用獨立 t 檢定 (independent t test) 來支持你的論點。例如,M&M 巧克力綠色比藍色好吃、女人永遠不會收到罰單、條紋衣服又開始流行等。t-test 源自於啤酒統計學家為了判斷啤酒製造過程中,裝滿整部升降機的穀物品質,因無法檢查所有穀物,故設法檢視隨機從較大的穀物母體抽出的一個小型樣本的方法。假設我們想驗證,女生永遠不會收到超速罰單:
| 罰單數 |
Group 1 (male) | Group 2 (female) |
平均數 (mean) | 1.71 | 1.35 |
變異數 (variance) | 0.71 | 0.25 |
樣本大小 (sample size) | 15 | 15 |
計算過程 |
t=Mean of Group 1 - Mean of Group 2Variance for Group 1Sample Size of Group 1+Variance for Group 2Sample Size of Group 2=1.71-1.350.7115+0.2515=1.42 |
< 5% 的機率偶然發生的 t 值 |
兩個群組加起來的樣本數 | 臨界 t 值 | 4 | 4.30 | 20 | 2.10 | 30 | 2.05 | 60 | 2.00 | 100 | 1.00 | | 1.96 |
t 檢定所回答的問題是,兩個樣本間發現的任何差異是否也存在與母體中,或是出於抽樣誤差。若 t 值 > 臨界值,我們就可以宣稱母體間有一種真正的差異存在。 因為 t = 1.42 < 2.05,沒有足夠證據顯示,男性真的比女性收到更多罰單,顯示樣本的差異,不代表母體也有會差異。 若你想知道任一群組平均是否大於另外一個,就會採用雙尾檢定 (two-tailed test),這通常也是我們感興趣的比較。 統計學家討論真實差異的方式是「這兩個樣本很可能取自不同的母體」。你我和研究員討論真實差異的方式很可能是「共和黨員與民主黨員有差異」或「這種藥物減低感冒的機率」。
|
【Hack #18】Find Out Just How Wrong You Really Are (找出你實際上錯了多少):如果你需要知道你有多接近真相,就該使用標準誤差 (standard errors)。例如,樣本的平均值是母體平均值很好的猜測值,問題是如何知道是否能相信你的結果,可透過標準誤差 (standard errors) 來調整你的準確度。
平均的標準誤差 (standard error of the mean) |
應用 | 用於「敘述統計」中,母體中某個變數的平均分數,例如,非終身聘教授的平均薪水。 |
公式 | Standard Error of the Mean = Standard DeviationSample size 隨著 sample size 增加,樣本平均就會更加接近真正的母體平均。意即,你對某樣東西觀測得越多,你的描述就會越準確。 |
意涵 | standard error of the mean 是樣本平均與母體平均的平均距離。 |
比例的標準誤差 (standard error of the proportion) |
應用 | 用於「抽樣調查」中,母體中具有某些特徵的比例,例如,誰會投票贊成我的 Frank 叔叔成為捕狗隊長。 |
公式 | Standard Error of the Proportion=(proportion)(1-proportion)Sample Size 隨著 sample size 增加,比例的標準誤差也會跟著縮小。隨著比例移離 .50,公式頂部的數字就會變小。 |
意涵 | standard error of the proportion 是樣本比例與母體中真實比例的平均距離 |
估計的標準誤差 (standard error of the estimate) |
應用 | 用於「迴歸分析」中的未來表現估計,例如,你訓練來做多選題測驗的寵物猴,可能的大學 GPA。用迴歸預測距離一個人會得到的實際分數有多遠。 |
公式 | Standard Error of the Estimate = Standard Deviation1-correlation2 standard deviation 是 criterion variable (因變數) 的標準差;correlation 是你的 predicors (自變數) 和 criterion variable (因變數) 間的相關性。 |
意涵 | 在此公式中,相關係數越大,估計的標準誤差就越小。估計的標準誤差是實際分數距離每個預測分數的平均距離。 |
此類工具可以讓你有信心地指出真相所在範圍,因抽樣誤差是常態分佈,標準誤差 (standard error) 也可以像標準差 (standard deviation) 那樣被用來定義常態曲線底下特定比例的分數。由於抽樣誤差是常態分佈,意味著這些大小的值在其範圍中的分佈符合常態曲線,讓我們產生那些有說服力的精確的信賴區間。 建立 95% 的 CI (信賴區間) | 標準誤差類型 | 標準差 | 樣本大小 | 樣本值 | 標準誤差 | 95%信賴區間 | 公式 (X: 樣本值, n: sample size) | 下限 | 上限 | 平均的標準誤差 | 15 | 30 | 100 | 2.74 | 94.63 | 105.37 | X1.96n | 15 | 60 | 100 | 1.94 | 96.20 | 103.80 | 比例的標準誤差 | 0.25 | 30 | 0.5 | 0.09 | 0.32 | 0.68 | X1.96標準誤差 | 0.25 | 60 | 0.5 | 0.06 | 0.38 | 0.62 | 估計的標準誤差 | 15 | 30 | 100 | 14.81 | 70.97 | 129.03 | X1.96標準誤差 | 15 | 60 | 100 | 14.65 | 71.29 | 128.71 | Frank 叔叔抽問 30 個選民,高達 50% 的人說會投票給他,經過此表格可發現,由於樣本數太小,選民會投給 Frank 叔叔的比例在 32% ~ 68% 之間,樂觀的 Frank 叔叔將此解讀為他可能會斬獲 68% 的選票,開始籌備慶功宴。 |
|
【Hack #19】Sample Fairly (公正地抽樣):透過具備科學根據的方式,可以再僅查看其中一小部分樣本的情況下,準確的描述整組東西。推論統計學 (unferential statistics) 能讓我們根據較小樣本的資料推論到一個較大的母體,不過為了讓一般化的推論有效,樣本必須公正地代表母體。以下為例,最外圈代表母體,40% 方形、20% 三角形與 40% 菱形;內圈則為樣本,形狀分佈比例剛好與母體一樣。如此就稱公正 (fair) 的樣本,恰好地代表母體。只有在樣本優良的前提下,推論才會有良好的結果,建構良好的樣本是推論的關鍵所在。計算完成後,可用【Hack #18】Find Out Just How Wrong You Really Are (找出你實際上錯了多少),判斷推論統計的誤差大小。
建構最佳的隨機樣本 | 說明 |
全宇集 (general universe) | 研究人員想要推廣泛化他發現的「抽象母體」。 例如,我想要描述有關所有漫畫書收藏家的一些事情。
|
工作宇集 (working universe) | |
抽樣單元 (sampling unit) | |
抽樣架構 (sampling frame) | |
抽樣常見名詞 | 說明 |
隨機 (random) | |
相等 (equal) | |
獨立 (independent) | |
真實世界的抽樣策略 |
抽樣策略 | 說明 |
便利抽樣 (convenience sampling) | |
系統抽樣 (systematic sampling) | |
分層抽樣 (stratified sampling) | |
群集抽樣 (cluster sampling) | |
判斷抽樣 (judment sampling) | |

|
【Hack #20】Sample with a Touch of Scotch (加水威士卡的抽樣):統計學家從母體選人做為樣本時,他們實際是從變數的連續分佈 (continuous distribution) 抽樣。不過有時候,把你的變數視為離散物件 (discrete objects) 而非離散分數,抽樣會更好懂一些。例如,若有一名研究人員感興趣的測量某種治療在一個連續 (continuous) 變數上的效應 (ex. 幸福感),他把幸福感 (happiness) 視為一個二分 (dichotomous) 變數,也就是幸福與不幸福,這是一種聰明的策略,因為把樣本視為代表大型的、離散的類別,而非更精確的連續值,可以讓關於抽樣的問題更容易回答與驗證。社會科學的研究統計者想要被說服他們的樣本能代表其母體,主要的考量永遠都會是他們樣本中符合特徵的比例,而非具有那些特徵的人數。最重要的是,那些關鍵研究變數每個分數的比例在樣本和母體中都相同。
【Hack #21】Choose the Honest Average (挑選誠實的平均):資料驅動的決策(例如,你是否能負擔在台北買一間房子,或你業務的核心市場包含了誰),經常仰賴「平均」(average) 作為一個大型資料集的最佳描述。問題在於,有三種完全不同的值都可以被標示為「平均」,而這些不同的平均經常會導致不同的決定,請使用正確的平均來做決策。
摘要值 (summary value) | 說明 |
平均數 (mean) | |
中位數 (median) | |
眾數 (mode) | |
如何挑選 honest average |
honest average | 說明 | 適用情況 |
平均數 (mean) | 是所有數加起來除以個數所得出的平均值。 | 如果分布相當對稱且只有一個眾數,就選擇平均數。 |
中位數 (median) | 將資料由小而大的順序排列,最中間的那個數即是中位數。 | 如果分布是傾斜的 (即有少數的離群值太大影響平均數),就要選擇中位數。 |
眾數 (mode) | 數值資料中出現次數最多的數值。 | 如果資料中有兩個或更多個趨勢 (trends),就該選擇眾數,並j為每個趨勢都回報一個眾數。 |
例子:假設班上有 15 名學生,每週零用錢分別為 80, 200, 120, 100, 130, 120, 90, 100, 150, 180, 100, 50, 2000, 100, 250,平均數 = 251.33,中位數 = 120,眾數 = 100。 |
【Hack #22】Avoid the Axis of Evil (避開邪惡軸心):表達數量、關係和研究結果時,圖形 (graphs) 是很強大的工具,但在錯誤的人手上,它們可能被用來欺騙人心。挑選誠實的圖表:
honest graphs | 說明 | 適用情況 |
長條圖 (bar chart) | X 軸代表類別或群組 (ex. 男性或女性),Y 軸則是連續的,bar 越高,變數 Y 的值就越高。 | 若 X 軸代表不同類別,而 Y 軸是連續的,就用 bar chart。 |
直方圖 (histogram) | X 軸代表連續的值 (ex. 月份),看起來像 bar chart,但是 bar 間沒有空格。 | 若 X 軸可被視為類別,但之間也具備某種有意義的順序,且 Y 軸是連續的,就用 histogram。 |
折線圖 (line chart) | X 軸與 Y 軸都是連續變數 (ex. 時間與價值),在任何點,線條所在位置越高,Y 軸所代表的數量就越大。 | 若 X 軸與 Y 軸都是連續變數 ,就用 line chart。 |
圖形例子 |
長條圖 (bar chart) |

|
直方圖 (histogram) |

|
折線圖 (line chart) |
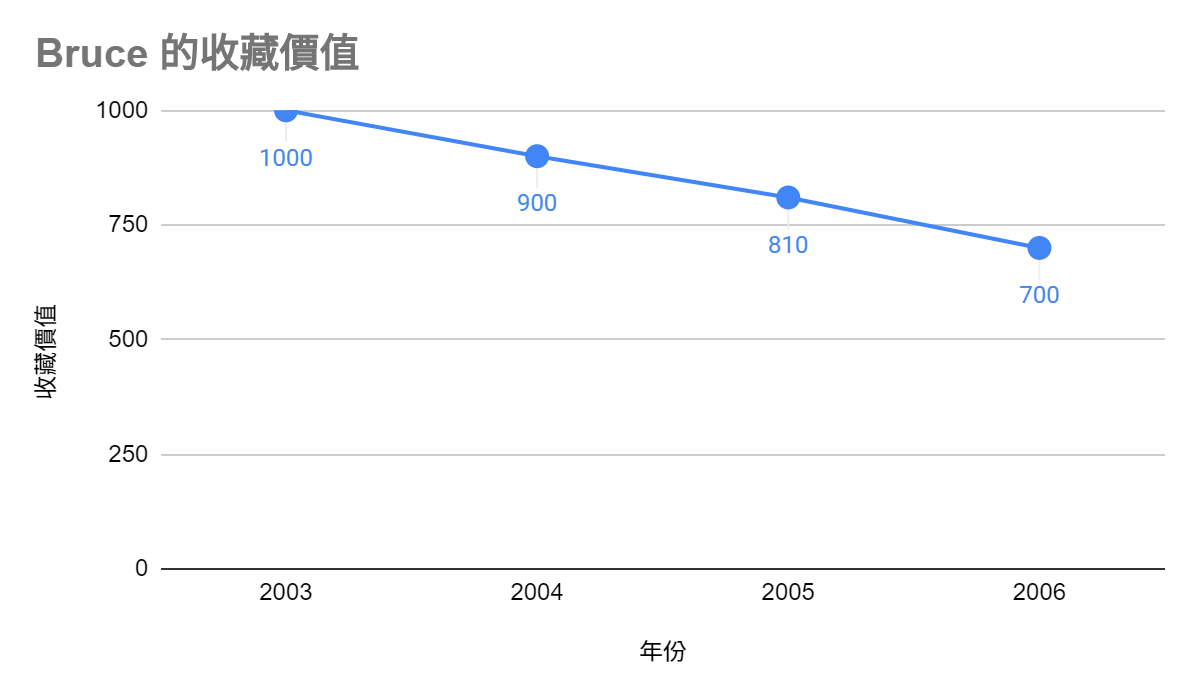
|
No comments:
Post a Comment