開發與善用 (Explore / Exploit) - 嘗試新歡?還是固守舊愛?
最佳停止問題的權威教科書一開頭就寫道:「最佳停止理論探討選擇適當時機採取特定行動的問題。」我們很難想出比這個更精確的言詞來描述人的境況。例如,我們決定買賣股票的時機、決定打開一瓶留給特殊場合的紅酒的適當時機、打擾某人的適當時機、以及接吻的適當時機。
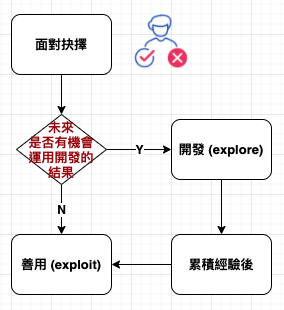
直覺上我們視為理性的決策方式,是毫無遺漏地列出各種選項,小心翼翼地加以權衡,最後選出一個最好的;然而,實際上,當時間不斷流逝,決策 (廣義的說是思考) 過程最重要的面相其實只有一個,就是何時該拿定主意。
我們在日常生活中,常遇到抉擇。原本只是想放鬆一下,但是想到要做抉擇,就又沒那麼輕鬆了。生活就是在創新和傳統、最新和最棒、冒險和堅持舊愛之間取得平衡。這正如找房子時,應按兵不動或採取行動的兩難局面一樣,真正的問題是:平衡點到底在哪?
| 選擇一 | 選擇二 |
去哪吃晚餐? | 去最喜歡的義大利餐廳? | 去剛開幕的泰國餐館? |
找誰一起吃飯? | 找最好的朋友去? | 找想進一步認識的普通朋友? |
點餐 | 點老樣子? | 點新菜色? |
開發與善用的權衡 (explore / exploit tradeoff):了解開發與善用後,不只有助於更正確決定上哪吃飯或聽什麼音樂,還能幫助我們了解應該如何隨時間而改變目標,並且知道合理的行動多半未必會選擇最好的目標。在權衡新事物和舊愛時,最重要的是我們打算在上面花多少時間?
| 開發 (explore) | 善用 (exploit) |
電腦領域的定義 | 蒐集資料 | 運用現有資訊取得已知的良好結果 |
特質 | 探索與發現新喜好的價值會隨時間而逐漸降低,因為我們體會它的機會越來越少。例如,你在阿姆斯特丹最後一晚到一家迷人的咖啡廳喝咖啡,日後再也沒機會光顧。 | 善用的價值會隨時間而逐漸提高,例如,今天你最喜歡的咖啡廳,跟你上個月的體驗差不多讚。 |
賭場的應用 | 如果你有時間善用到開發結果,就選擇開發 (ex. 哪台吃角子老虎比較好賺) | 如果你打算離開賭場,就選擇善用 (選擇已知勝率最高的吃角子老虎機) |
其他生活的例子 | 樂評家聽新作品,寫評論 | 家人在假日聚在一起吃飯;聽喜愛歌手的演唱會 |
|
製藥業的兩難
開發 (explore) | 善用 (exploit) |
探索不確定的未來,希望永續經營,若有重大醫學突破,可以持續幫助未來的人類。 | 確保現在能賺進利潤的現有產品有很好的表現。
不論怎麼想,「現在」總是比未來重要,利潤更是如此,經濟學家把「現在比未來有價值」稱為「折現」。
舉例來說,你對於明天晚餐的關心程度遠高於一年後的晚餐,確切的差異取決於你的「貼現函數」。 |
Gittins Index 說明
提出者 |
英國數學家 John Gittings 於 1970 年提出此指數,破解數十年來無法解達的數學謎題。 |
白話說明 |
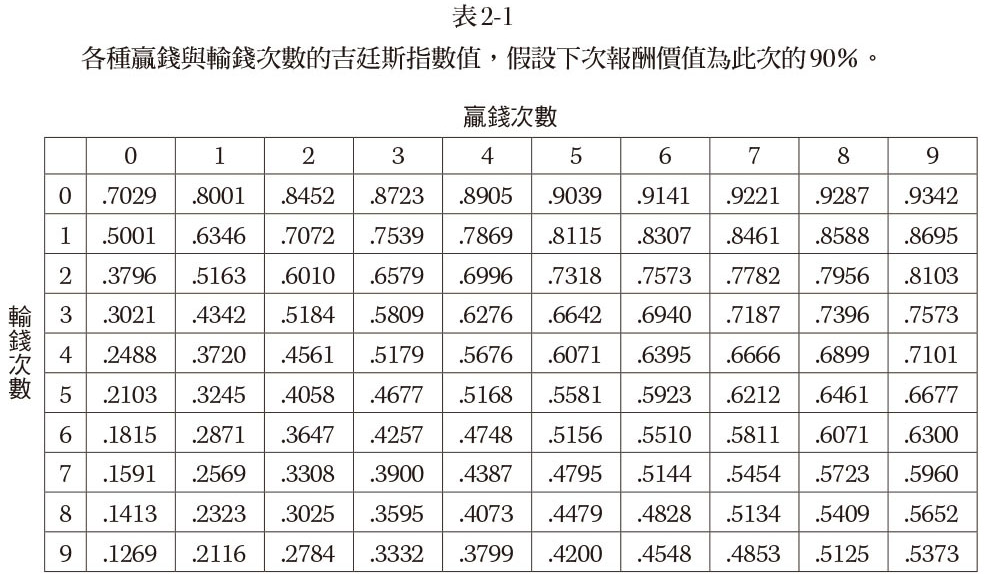
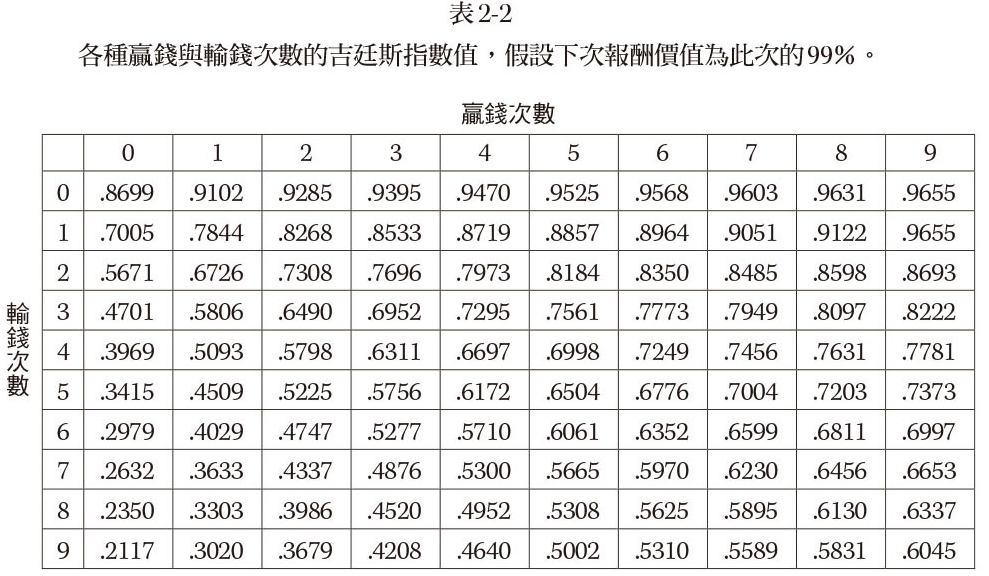
當你計劃出去吃一頓飯的時候,明天那頓應該比今天這頓要貶值一點 —— 因為你明天可能會離開這裡,吃不上那頓飯。具體貶值多少,取決於你預期還能停留多長時間。基於這一點,他提出了一個非常複雜的解決方案,最後結果是給每個選項計算了一個指數,現在被稱為「Gittins Index」。 (Ref.: https://reurl.cc/1gZmkX) |
Gittins Index 表格說明 (表 2-1) |
|
Gittins Index 表格說明 (表 2-2) |
|
理論限制 |
|
反思 |
|
生活智慧應用 |
① 年輕時代要大膽探索,因為你還有時間:年輕時可不斷探索未知,積累經驗教訓,才能迅速理解這個世界,後期才能做出更好的選擇。 ② 隨著年齡增長,要慢慢學會利用已有的經驗,專注於收獲:一般人的規律是,人的年齡越大,社交的圈子越窄。這其實是老人的理性選擇。他們已經完成了探索!知道自己最適合做的事情是什麼,和哪些人在一起最舒服,哪個餐館最符合自身口味,已沒有冒險探索的必要,只要享受人生就行了。 ③ 慢慢變老的過程中,我們的生活其實是越來越好:老人不探索,並不是不敢探索,而是因為他們不用探索 — 他們已經完成探索。當你看到一位老人,每天跟同一個人,去同一個餐館,坐在同一個座位,點同樣的飯菜,你可能以為他的生活很無聊 —— 殊不知這才是最浪漫的事,他是在享受自己用一輩子的時間所探索出來的成果!
|
當 Gittins Index 對你來說太複雜,你還有一個選擇:特別注意「遺憾」。遺憾常源自於我們沒做到的事,以及沒嘗試過的事。管理理論學家 Chester Barnard 曾說:「放手嘗試的話,就算不成功你至少還有收穫 (to try and fail is at least to learn);但沒嘗試就沒有結果,這樣的損失難以估計。」
A/B Test (Ref.: https://reurl.cc/1gZGLV)
定義 |
AB 測試 (A/B test) 是許多網站、尤其是具備電子商務功能的網站拿來快速測試改版、微調效果並協助設計與商業決策的方法之一。簡單來說就是將欲測試的變因或假說分別做成A版與B版 (甚至C、D等版),利用一些工具,將造訪網站的人流隨機均分至兩個版本,最後選擇目標達成表現較好的版本。 |
統計學角度 |
從上面的定義,我們可以知道 A/B 測試其實包含了三個核心概念:「隨機化的實驗」、「一個變因,兩種選擇」、「兩種樣本的假設檢定」。以統計學中實驗設計的角度來看,進行A/B 測試實際上是在執行一個「隨機對照試驗」 (Randomized Controlled Trial,RCT):在所有的使用者中隨機抽出兩組,一組投放 A 版本,另一組投放 B 版本,其中 A 版本與 B 版本只有一個地方不一樣,接著蒐集使用者的資料,並進行分析比較出哪一個版本較佳,這便是整個A/B 測試的過程。在進行 A/B 測試時的步驟如下: 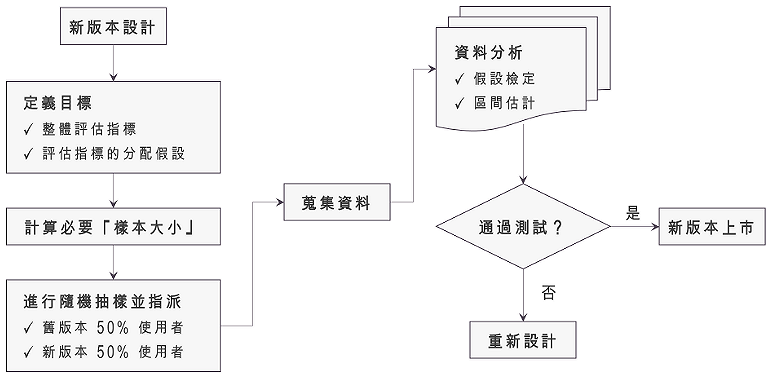
|
大致來說,大多數人傾向過度開發,也就是對新事物的偏好遠大於原本最喜愛的事物。所以,我們常太早決定用誰擔任新秘書,但又常常太晚決定不再嘗試新航空公司;沒有祕書需要付出代價,太早決定只選某家航空公司也是。
要在變化不定的世界生活,本身也要有變化不定的特質。只要事物持續改變,你就不能完全停止開發,例如,你先前感到失望而幾年沒去過的餐廳,或許已經換人經營,可能可以再訪一次。
開發與善用的矛盾、時間的重要性、Gittins Index 表格中 0-0 選項的高勝率、盡量減少遺憾等,不僅讓我們以新方式理解自身面臨的特定問題,也能了解人類生活的所有層面。
人類有個奇怪的特質,就是我們需要花費多年才學會自立;反觀動物,北美馴鹿與羚羊打從一出生就要開始逃離掠食者。
玩吃角子老虎機 | 育兒 |
最佳策略通常是一開始先開發,再依據開發 (explore) 結果善加利用 (exploit) 勝率較高的機台。這種方式的缺點是,開發階段的報酬通常不理想。 | 童年時期讓我們有機會開發各種可能性,不用擔心報酬,將報酬問題交給父母、祖父母來處理。
兒童的善用能力 (exploit) 很差,不會穿鞋子、不懂長期計畫、很難專注,各方面都不在行;但是對新玩具很感興趣,很擅長按下隨機按紐 (explore),從 A 跳到 B。
如果說兒童時期的目的是開發,他們確實應該做上述的事情。嬰兒很會把每個東西都放到嘴裡嘗嘗,就跟大人在賭場裡每部吃角子老虎都拉拉看一樣。 |
更廣泛地說,我們對理性的直覺通常源自善用而非開發。我們討論決策時通常只注意單一決策的立即報酬結果,如果我們把每個決定都當成最後一次,採取善用決策確實合理。但是我們一輩子要做出許多決定,其中許多決定、尤其是在人生初期來說,強調開發 (例如,捨棄已知事物而選擇新事物、捨安全而選擇刺激、捨考慮而選擇隨機),才是最合理的選擇。
老人的社會關係減少,是他們自己選擇的。他們選擇削減次要關係,轉而專注於少數親近的朋友和家庭成員。這個過程是刻意的選擇,人類接近生命終結時,往往希望更專注於更具意義的關係。但是,老人與年輕人都是依據自己的時間做出最適宜的選擇。刻意把社會網絡限縮到只留下最具意義的關係,是享受剩餘人生較少時的合理反映。但並非老人永遠都是選擇善用,年輕人永遠都選擇開發:
選項 | 年輕人 | 老人 |
選擇飯友 | 【開發】 傾向選擇新朋友 | 【善用】 傾向選擇家人或老友 |
選擇是否搬到國外 | 【善用】 傾向選擇家人留在家鄉 | 【善用】 傾向選擇家人留在家鄉 |
選擇是否選擇新的醫療技術,讓自己延年益壽 | 【開發】是 | 【開發】是 |
如果把未來的人生視為好好運用幾十年來累積的知識的機會,最大的收穫應是這句話:開發者用樂趣換取知識,人生應該越過越好。