排程 (Scheduling) - 優先的事情優先處理
亞里斯多德曾說:「我們經常做什麼事,就會變成什麼樣的人 (We are what we repeatedly do)。」你想拖地板、多花點時間陪孩子、趕在期限前報稅、還有學法文。你應該在什麼時候用什麼順序做哪些事?《Get Things Done》(搞定) 建議,如果一項工作時間只花你兩分鐘以內,想到就馬上去做;《Eat That Frog!》 (想成功,先吃了那隻青蛙) 建議先處理最難的工作;《The Now Habit》(十招克服惱人的拖延) 建議先安排個人社交活動與休閒,再把工作填進空檔;《Wait》(等待的技術) 建議刻意不要馬上動手處理工作。每位大師說法都不同,很難決定該聽誰的。
在電腦科學的領域,在擬定排程計畫前,必須先選擇「測量標準」。我們所選擇的測量標準,將直接影響哪種排程方法表現最好。以有期限的工作為例,最常見的標準是延遲程度;在零售業或服務業中,則是客戶可能會不高興的程度,客戶等待時間越長就越不高興。
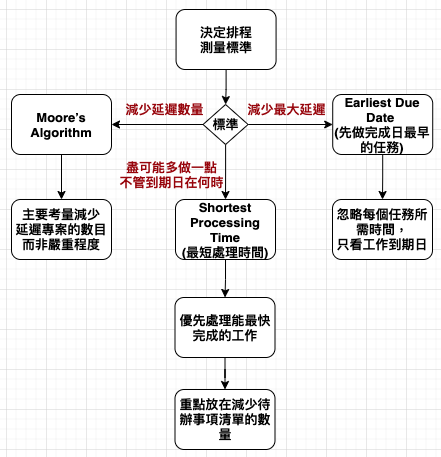
最短處理時間 (SPT, Shortest Processing Time) 告訴我們,優先處理能最快完成的工作。即使客戶沒緊盯你每件工作的進度,完成所有工作所需的總時間無法改變, SPT 或許可以盡可能快速減少待處理工作的數目,SPT 此法完全把重點放在減少待辦事項清單的數量。如果每件未完成工作就像背上的一根刺,那麼盡快解決最容易的項目,可以讓你感到安心。
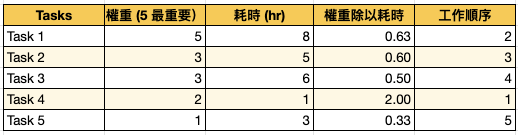
待辦事項的重要性,並非每樣都相同。要是廚房起火,滅廚房的火雖然會比較費時,還是要先做,完成後再做其他事。在重要程度的差別是以權重 (weight) 這個變數來表示,你只要稍微調整 SPT 的策略即可:把每項工作的權重除以完成所需時間,再從每單位時間重要性最高的工作開始,依序處理到最低的工作。雖然日常生活很難指定重要程度,但此策略仍提供不錯的基本法則,除非重要性兩倍多,不要把耗時兩倍的工作放在前面。
在商場上,權重或許可以輕易轉化為每項工作所能賺進的金額。例如,假設你是自由工作者或是顧問,把每個專案的費用除以工時,先從時薪最高的工作一次做到最低的即可;動物覓食也是如此,牠們會依照食物熱量與取得即時用時間的比例高低來覓食。
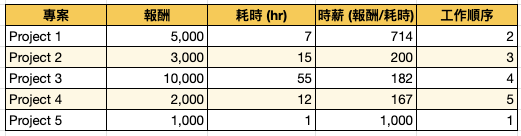
將上述原則套用至還債
目標 | 策略 | 著重點 |
減輕負債總負擔 | 雪崩式償債 (debt avalanche) | 不管負債金額與數目,一律把錢用來償還利率最高的負債,讓銀行帳戶由負轉正的策略,盡可能幫你減少負債總負擔。 |
減少負債數目 | 雪球式償債 (debt snowball) | 你覺得處理一大對帳單和街催收電話的麻煩,比利率差異更難忍受,回歸不加權,採取 STP 原則,優先償還金額最少負債,快速減少負債項目數 |
我們常認為拖延是懶惰或逃避行為,但想認真熱情地盡快完成工作的人,也可能有此傾向。拖延其實是人類急欲完成次要目標,即使必須花費更多時間或體力也在所不惜。先執行瑣碎工作而延遲真正重要的工作的行為,就是「急欲完成次要目標」的例子,因為他只想盡快減少心中的待辦事項,但不能說他的工作執行策略不好,只是評估成果的標準跟他們想的不同。電腦遭受攻擊也會出現拖延傾向,例如電腦受到 ping 攻擊或阻斷式攻擊 (DDoS) 時,就是駭客命令系統執行一大堆瑣碎事情,使系統無法處理真正重要的事情而癱瘓。
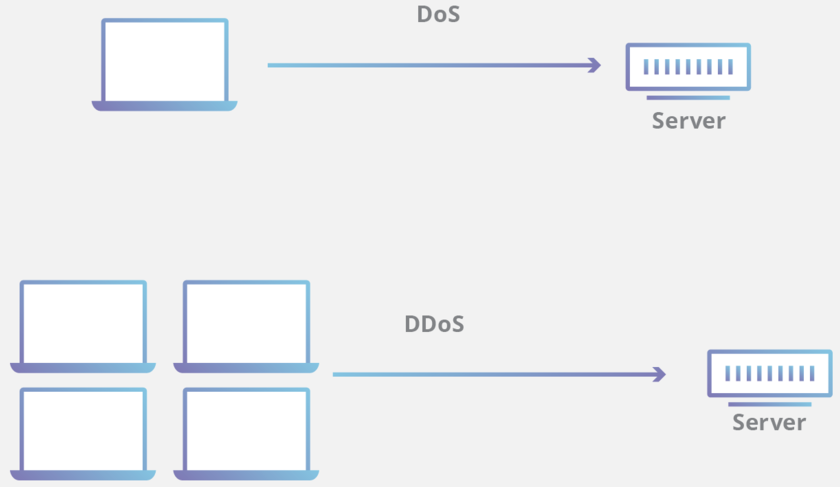
(Ref: https://reurl.cc/WED0m5)
評估標準能載舟也能覆舟,若所有工作擁有相同權重同,採用「最短處理時間法 (SPT, Shortest Processing Time)」就是合適的策略。
Priority Inversion (優先權倒置) 與 Priority Inheritance (優先權繼承)

雖然說,最重要的事不容許被不重要的事影響,但有時候得先做不重要的事,才能完成最重要的工作,你還是得先做此前置工作,排程專家稱之為優先權限制 (priority constraint)。運營研究專家 Laura Albert 時時記住這個原則以處理家事:「整天跟三個小孩在一起,要安排很多事,孩子們要吃完早餐才能出門,要是我忘記拿湯匙給他們,就無法吃早餐,接著就無法出門。有時,忘記一件小事就會耽誤所有事情。」
以租車搬家為例,雖然還車時間到期時,還車是最重要的事,但若未完成搬家,還車後你就無法繼續搬家,你應選擇延遲還車時間,才是正確的決策:

若延遲的工作任務中,彼此權重皆相同時,可採取 Moore’s Algorithm 來盡量減少延遲數量,但是當權重不同時,就會變成難解的排程難題。此時可以用 preemption 讓工作中途停止,讓遊戲規則大幅改變。
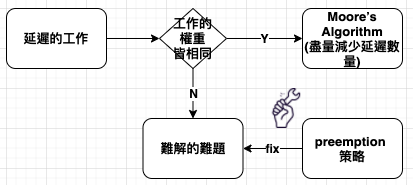
Preemption (流程搶占) 策略:最早到期日策略 (EDD, Earliest Due Date) vs 最短處理時間策略 (SPT, Shortest Processing Time)

在真實世界,無法確切未來一周的完整工作項目,很可能電話隨時響起、或突然來封 e-mail 通知而增加新工作。即使在不確定的情況下,最早到期日與最短處理時間仍是最佳策略,讓我們盡可能有最佳表現。
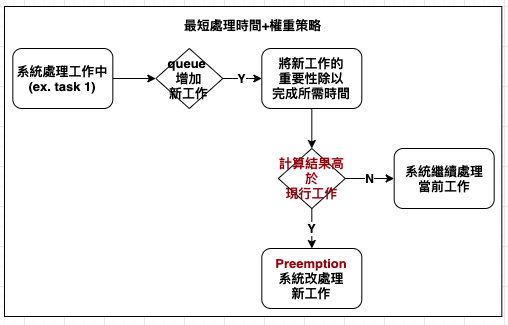
商管作家與程式設計師 Jason Fried 說:「你覺得沒有十全十美的計畫就無法著手嗎?把計畫換成猜測 (replace plan with guess),輕鬆面對就好。」感覺混沌不明時,你需要的不是行事曆,而是待辦事項。「最短時間加權法」可說是不確定狀況下的最佳通用排程策略的選項之一,是排程理論中的瑞士刀:一出現新工作,就把它的重要性除以完成所需時間,如果結果高於正在進行的工作,就做新工作,反之則繼續進行當前工作。

人與電腦在排程都遇到類似的挑戰
排程挑戰 | 說明 |
① 執行排程與接受安排是同一部機器 | |
② Preemption 需付出代價 | Preemption 不是白吃的午餐,每次變換工作都會付出代價,在電腦科學稱為 context switch。 例如,程式設計師暫時放下手邊工作,去修正另外一個功能的 bugs,當修正結束後,再回頭進行原本的工作,他須先找出原本做到哪裡後,才能繼續進行,這些過程都是「虛功」,不會帶來任何實際進度,完全都是內耗與空轉,context switch 的耗時全部都是浪費。 心理學家已證明,切換工作對人的影響可能包含延遲和錯誤 (delays and errors),影響會多達數分鐘,而不是數秒鐘。更具體的說,如果你在一小時內打擾某個人好幾次,他的工作可能會完全無進展。 匹茲堡大學排程專家 Kirk Pruhs 曾說:「如果時間不到一小時,我只會做一些瑣事,因為我得花 35 分鐘才能搞清楚要做什麼,接下來就沒什麼時間做了。」
|
電腦的 multi-thread 運作方式很像拋接雜耍員,每次只拋一顆球,但有三顆球同時在空中;電腦 CPU 也是如此,每次只執行一個程式,但在好幾個程式間快速切換 (僅萬分之一秒),所以看起來能同時撥放 YouTube、瀏覽 Facebook 與通知你有新的 Line 訊息。假設拋接雜耍員的上限是四顆球,若多給一顆球,他沒接到的不只是第五顆球,而是全部的球都掉地上;電腦系統也是如此,額外加一個新程式超過系統負荷時,此舉會讓整個系統當掉 (complete collapse of system),你可能不知道臨界點在哪,但超過當掉時就會知道。
每項工作都會佔據你一點注意力,當你想暫停手上所有工作,才能寫下所有要做的事情時,就表示你已陷入 context switch。人類的認知資源有限,當記住必須做的所有工作占據你全部的注意力,或是設定每項工作的優先權耗光執行工作的所有時間,或是我們的思緒經常在化成行動前就受到干擾,這就是陷入 context switch,你的大腦因活動過度而癱瘓。電腦可以增加 main memory,以減少 context switch 花費的時間;人類則受限於有限的認知資源。
反應能力是你的回應速度,處理能力是你總共能完成的工作量。具備良好反應能力的人,未必擁有同樣良好的處理能力。兩者的取捨很不容易,矛盾的是,完成作業的最佳策略反而是慢下來。設定每項作業的最短執行時間,有助於防止為了確保反應能力而完全忽視處理能力。

若讓最短執行時間大於 context switch 的時間,系統就絕對不會把所有時間花在 context switch 上。固定時間長度 (timeboxing) 或番茄工作法 (pomodoro) 這類使用計時器設定一段時間只做一件事情,就是實現這樣的概念。
當處理能力越高,反應能力就會越低。例如,當你越專心工作於某件事,越久沒檢查 e-mail,對於 e-mail 反應能力就會越低。對於電腦來說,只要使用者不覺得停頓或緩慢,就盡可能延長時間;對於人類來說,盡可能延長單一工作的執行時間,但不要使反應能力低於可接受的限度。所以,你要先決定好自己的反應速度,接下來如果希望好好完成工作,就不要讓反應能力高於此程度。
若你發現手上許多短時間工作,因此常需要做 context switch 時,可採源自電腦科學的 interrupt coalescing (中斷聚合) 概念。舉例來說,假設你有五張信用卡帳單,依據最晚結帳時間設定繳費日,在該繳費日坐下來一次處理所有帳單,不管帳單是 1 天前、3 星期前送達都沒關係;又如郵局的投遞週期也是 interrupt coalescing,國內快捷郵件本地 (同一郵遞區號)互寄,15時前交寄當日投遞;主要都市間互寄,11時前交寄當日投遞,逾11時交寄第2日上午投遞。