推論統計學 (inferential statistics) 是完全基於機率本質的一門科學,能幫助我們理解事情運作的方式、發現變數之間的關係、在只看到一小部分時就能描述龐大的母體 (popuplation)、作出精準的預測,甚至能幫你下對注來賺點錢。
本書所提供的實用工具來自統計學 (statistics)、教育與心理測量 (educational and psychological measurement) 和實驗研究設計 (experimental research design) 領域,為社會科學、商業、遊戲與賭博等領域中的各種問題提供了解決方法。
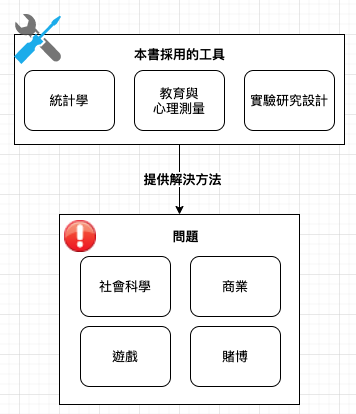
書籍論述架構
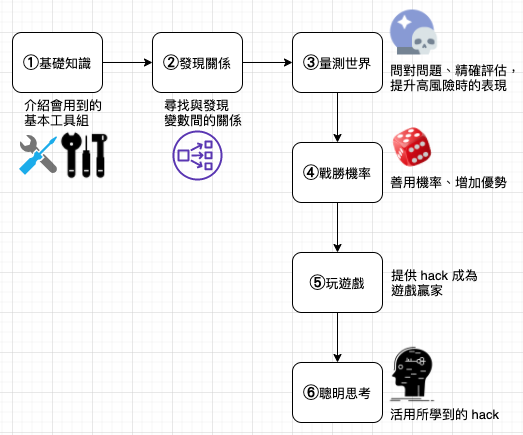
統計學 10 個基礎知識 (The Basics)
Hacks #1 ~ #10 | 說明 |
① 得知大秘密 | |
② 僅用兩個數字描述世界 | |
③ 找出機率 | |
④ 反駁虛無 | |
⑤ 增加樣本數,縮小誤差 | |
⑥ 精確測量 | |
⑦ 測量水平 | |
⑧ 提升威力 (檢定力) | |
⑨ 顯示因果關係 | |
⑩ 識別出重大發現 | |
【Hack #1】得知大秘密 (Know the Big Secret):統計學的目標,是對樣本分數 (samples of scores) 做出機率陳述 (propability statements)。
名詞解釋 | 說明 |
樣本 (samples) | |
分數 (scores) | |
機率陳述 (propability statements) | 統計學家把關於某些值的分布 (distribution) 之已知資訊 (known information) 表達為機率陳述。分數的分布 (distribution) 是所有不同的數值所組成的列表,有時候還列出每個值各出現幾次。 例如,如果你知道你修的一堂課的小考分數分布中,有 25% 的同學得到 10 分,我就可以說你有 25% 的機率「得到」 10 分,也可以說你有 75% 的機率「沒得到」 10 分。
|
【Hack #2】僅用兩個數字描述世界 (Describe the World Using Just Two Numbers):大多數的統計解法或工具之所以行得通,是因為你可以檢視樣本,並對較大的母體作出準確的推論。中央極限定理 (Central Limit Theorem) 則是用來調整這些工具的工具。
基礎知識 | 說明 |
樣本與母體 | 在推論統計學中,整組分數中你能看到的那個部分就稱為樣本 (sample),而你想要出做推論的那整體分數就是母體 (population)。 
|
平均值 (mean) | 是所有樣本值的算術平均數 (arithmetic average),此一數字被稱作是這一組樣本分數的集中趨勢 (central tendency)。 |
標準差 (Standard deviation) | (x - Mean)2n - 1 |
中央極限定理 | |
中央極限定理是機率論中的一組定理。中央極限定理說明,在適當的條件下,大量相互獨立隨機變數的均值經適當標準化後依分布收斂於常態分布。這組定理是數理統計學和誤差分析的理論基礎,指出了大量隨機變數之和近似服從常態分布的條件。(http://shorturl.at/ghBFO)
百分等級 (PR, Percentile Rank) 與 百分位數 (以 Pk 表示第 k 百分位數)
百分等級 (PR, Percentile Rank) | PR = 100-(100 R - 50N), R : 排名, N : 總個/人數 PR = (100N贏過的人數)+(100N12), N : 總個/人數 |
百分位數 | 以 Pk 表示第 k 百分位數 計算當PR值多少時,要考幾分
|
首先將班級原始分數由低至高排列,例如班上 10 個學生的分數分別為:
成績 | Rank | 從排名推算 PR | 贏過 幾個人 | 從贏過幾個人推算 PR | 百分位數(Ppr)(Pp) 要考幾分 |
35 | 10 | 100-10010-5010=5 | 0 | 100100+1001012=5 | 35 |
56 | 9 | 100-1009-5010=15 | 1 | 100101+1001012=15 | 56 |
62 | 8 | 100-1008-5010=25 | 2 | 100102+1001012=25 | 62 |
71 | 7 | 100-1007-5010=35 | 3 | 100103+1001012=35 | 71 |
76 | 6 | 100-1006-5010=45 | 4 | 100104+1001012=45 | 76 |
78 | 5 | 100-1005-5010=55 | 5 | 100105+1001012=55 | 78 |
83 | 4 | 100-1004-5010=65 | 6 | 100106+1001012=65 | 83 |
84 | 3 | 100-1003-5010=75 | 7 | 100107+1001012=75 | 84 |
90 | 2 | 100-1002-5010=85 | 8 | 100108+1001012=85 | 90 |
96 | 1 | 100-1001-5010=95 | 9 | 100108+1001012=95 | 96 |
假設同學 A 考 84 分,透過排名計算 PR =100 - (100 3 - 5010) = 75 透過贏過幾個人計算 PR =(100107)+(1001012)=75 若同學 A 的 PR 值為 75,百分位數計為P75 ,則 P75 的原始分數為 84。 https://bit.ly/31uvgNB |
【牛刀小試】某位學生在滿分 100 分的考卷得到了 68 分,相較於全校同年級 1,000 位學生的成績,該生的百分等級為 40,在同班級 50 位學生中算是第 10 高分
該生在其班級的 PR =100-(10010-5050)=81 該生同班同學多數人的成績在全校學生中算是比較偏低的 該校同年級學生成績第 40 百分位數(P40)為 68 分 |
百分等級和Z、T分數的差異比較 (https://bit.ly/2XsNopQ)
| 百分等級 (PR) | 標準分數 (Z、T分數) |
單位 | 將群體分成100等分 | 以標準差作為單位 |
數值 | PR值永遠為正數 | 數值可以為負數 |
量尺 | 次序量尺 | 等距量尺 |
Z 分數與 T 分數 (https://bit.ly/2XsNopQ)
Z Score (Z 分數) | T Score (T 分數) |
將原始分數以「在平均數之上或之下幾個標準差」的方式表示分數,意即我們可以透過 Z Score 知道個體位於群體中的相對位置。 | T 分數是 Z 分數的衍生分數,是 Z 分數藉由直線轉換產生的分數,通常為 Z 分數的10倍加上50
|
Z=x - 註:μ為母體平均數 σ為母體標準差 | T=10Z+50 |
假設學生 A 此次數學考了90分,班上平均為80分,標準差是10分
Z=90-8010=1
Z=1 表示學生A的分數比全班平均多了"1"個標準差;假設小美這次考70分,Z分數就是-1,也就是比平均數還少"1"個標準差
Z分數的正負可以判斷個人的成績是否高於平均數,而Z分數的絕對值可以判斷距離平均數的差距有多遠。 | T Score 是為了解決 Z Score 有小數以及負數的問題,是為了方便計算
T=101+50=60
|
無論原始分數分配為何,轉換後分數分配皆為常態分配 |
平均數兩邊各含3個標準差,亦即最高標準分數為+3,最低標準分數為 -3。標準分數與平均數的差數,即表示該一分數在平均數之上或下幾個標準差,可以正確說明該一分數在群體中的位置。 如某應考人原始分數經換算標準分數後為 2.5 ,表示該應考人的分數在平均數以上 2.5 個標準差 ,在整個得分分配中,是很好的成績。原始分數經轉換為標準分數後,不同科目的成績、不同單位的數量,均可直接比較或相加、相減及平均,不會受評分寬嚴及試題難易的影響。因原始分數轉換為標準分數後,常成小數或負數,為免計算困難,通常將標準分數乘以一個常數,再加一常數,使成整數。最常見的方法為標準分數乘10,再加50。亦即設定標準差為10,平均數為50。經此一轉換,即成 McCall的 T 分數。(https://bit.ly/2Dx694l)
【Hack #3】找出機率 (Figure the Odds):贏得樂透的機率?同一天被閃電劈到又被車撞的機率?判斷某件事情發生的可能性並回答這類的問題,正是統計學的核心所在。計算機率的基本法則能讓統計學家預測未來。以下兩個工具就足以回答日常生活中大多數的「機率有多少?」問題,可用來回答某件事情發生可能性 (likelihood) 的機率 (probability)。
機率法則 | 說明 |
加法法則 (Additive rule) | 數個獨立事件 (independent events) 中任何一個發生的機率就是每個事件的機率的總和 (sum)。 |
乘法法則 (Multiplicative rule) | 一連串的獨立事件全都發生的機率就是每個事件的機率之乘積 (product)。 |
加法法則:如果完成某件事的方法可區分成 k 個類別, 而第 j (j = 1, 2, 3, …, k) 個類別有 mj 種方法, 且每個類別互不相干, 那麼完成這件事的方法共有 m1 + m2 + m3 + … + mk種。(http://shorturl.at/gmBGT)
應用題 | 解題 |
從甲地到乙地有飛機、火車與巴士等三種交通工具可到達,其中飛機每天有 3 班,火車每天有 15 班,,巴士每天 25 班,若A先生欲從甲地至乙地,有幾種交通班次可選? | A先生只能選擇一種交通工具的某個班次,共有 3 + 15 + 25 = 43 個交通班次可選擇 |
假設某期刊室內,有5種週刊、4種月刊、3種季刊供民眾閱讀,今甲生從這些期刊中任選一種,試問共有幾種不同的選法。 | 甲生一次只能選一種,共有 5+4+3=12種選法 |
某校想了解學生對法律常識的認識, 想從該校高三有 20 班,高二有 19 班, 高一有 18 班,任選一班進行法律常識測驗, 試問共有幾種不同的選法? | 20+19+18=57種選法 |
乘法法則:如果完成某件事情可依序分成 k 個步驟, 而第 j (j = 1, 2, 3, …, k) 個類別有 mj 種方法可以完成它, 那麼完成這件事的方法共有 m1 ✕ m2 ✕ m3 ✕ … ✕ mk 種。假設某教室內有 n 張椅子, 有 n 位學生依序選擇座位,試問共有幾種不同的選法? 我們通常會將 n ✕ (n-1) ✕ (n-2) ✕ … ✕ 2 ✕ 1用 n! 來表示。讀做 "n階乘"。(http://shorturl.at/gmBGT)
應用題 | 解題 |
某兔穴有進出口四處,一兔由不同一口進出的方法共有幾種? | 共 4(4-1)=12種 |
假設某教室有四張椅子, 甲、乙、丙、丁四位學生依序選擇座位, 試問共有幾種不同的選法? | 共4(4-1)(4-2)(4-3) = 24種選法
|
某速食店舉辦週年慶,提供主餐 5 種, 副餐 4 種,飲料 6 種,,任選主餐、副餐與飲料各一種,特價 70 元,試問顧客有多少種選擇的方式? | 共 546=120 種選擇 |
甲、乙兩人在排成一列的8個座位中相鄰而坐,試問共幾種不同的坐法? | 2(8-1)=14種 |
機率學術語:10 次之中有 1次發生的機率,有三種回答方式
三種回答方式 | 說明 |
以百分比回答 (percentage) | 10 次中有一次可被表達為 10% |
以勝算回答 (odds) | 10 次中有一次這種情況的勝算是 9 對 1,也就是 9 次輸的機會相對於 1 次贏的機會 |
以比例回答 (proportion) | 10% 可被表示為 0.10 |
獨立擲骰子結果之機率
擲出 | 結果數 | 機率 |
2 | 1 | 0.028 |
3 | 2 | 0.056 |
4 | 3 | 0.083 |
5 | 4 | 0.111 |
6 | 5 | 0.139 |
7 | 6 | 0.167 |
8 | 5 | 0.139 |
9 | 4 | 0.111 |
10 | 3 | 0.083 |
11 | 2 | 0.056 |
12 | 1 | 0.028 |
總計 | 36 | 1.0 |
情境 | 計算方式 |
假設從 result set 中,10, 11, 12 其中之一才算獲勝,這樣取得其中一中的勝率為何? | 把 10, 11, 12 的機率加總起來,就是你的勝率 = .083 + .056 + .028 = .167 此處用「加法原則」,因為你感興趣的是數個獨立事件 (independent events) 之中任何一個是否會發生 |
假設一系列連三次擲骰子,連續出現 10, 11, 12 的機率為何? | 因為你感興趣的是數個連續事件是否全部 (all) 會發生,所以會用「乘法原則」,機率 = .083.056.028=.00013 |
我們的機率陳述其實關於的是過去,而非對未來的預測。你可能會假設過去事件能讓我們對未來有個不錯的認知,但誰又能確切知道呢?
【Hack #4】反駁虛無 (Reject the Null):實驗科學家取得進展的方式就是做出他們確信不正確的猜測。科學是由目標驅動的過程,而目標就是建構出關於世界的知識體系。實驗科學透過一組叫做假設檢定 (hypothesis testing) 的邏輯步驟來引進新的定律和理論,並檢驗它們。而一個假設 (hypothesis) 是關於世界的一個猜想 (guess),它是可測試的 (testable)。研究假設檢定的課能結果:
| 檢定結果 |
接受 H0 | 拒絕 H0 |
事實 | H0 為真 | 正確判斷 | 檢定結果做了 錯誤的拒絕 type I error (𝞪) |
H0 為偽 | 檢定結果做了 錯誤的接受 type II error (β) | 正確判斷 |
- 統計學家測試虛無假設 (null hypethesis),是因為要證明某件事情是真的,是非常困難的。證明一個經過的猜想是錯的,比證明一個精確的猜想是真的,要容易得多。對專業統計學家來說真是個好處,他要做的只是告訴你,你的答案是錯的,而非告訴你正確答案是什麼。