假設檢定流程 (http://shorturl.at/jmyzM)
假設檢定流程 | 說明 |
提出相關的虛無假設和對立假設 | |
選擇檢定統計量 | 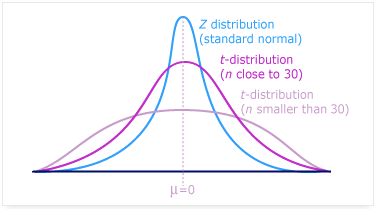
|
選擇顯著水準並決定決策法則 | |
比較樣本統計量與臨界值並下結論 | |
【Hack #5】增加樣本數、降低誤差 (Go Big to Get Small):縮小你抽樣誤差 (sampling error) 最好的辦法就是增加你的樣本大小 (sample size)。這也是所謂的大數法則 (Law of Large Numbers),人們發現,在重複試驗中,隨著試驗次數的增加,事件發生的頻率趨於一個穩定值;人們同時也發現,在對物理量的測量實踐中,測定值的算術平均也具有穩定性。大數法則的描述只出現或採樣都是「隨機 (randomly)」 的情況下成立。
大數法則應用 | 說明 |
賭博 | 若在單一次試驗中,某個事件有一特定的發生機率,當執行無限次的試驗時,出現的比例就會接近那個機率。 |
誤差 | 樣本平均與母體平均之間的差異,會隨著樣本大小接近無限大而遞減、靠近零。 |
影響 | 樣本所代表的母體中重要的特性之數目會隨著樣本大小變大而遞增,就跟他們估計值的準確度一樣。 |
【Hack #6】精確測量 (Measure Precisely):古典測驗理論 (classical test theory) 能為任何測驗中組合起來產省一個分數的那些要素做出不錯的分析。這個理論有一個實用的意義是,測驗分數的精準度可以被估計並回報。
Observed Score = True Score + Error Score
受試者的真實值或真正能力是無法直接觀察的,只能由測量的方式去找出觀察值或觀察到的能力。這種觀察值含有誤差,而此誤差被假設為一個隨機(random) 變數,其分配是以零為集中趨勢指標的常態分配。這種誤差有時大於真實值也有時小於真實值,但總平均起來誤差為零。由於此隨機誤差的存在,因此即使受試者的真實值 (T) 是固定不變的,每一次的觀察值卻不一定都相等,不過觀察值的分配亦為常態分配。(古典測驗理論)
方程式組成元素 | 說明 |
觀察到的分數 (Observed Score) | 在一個測驗實際回報的分數,通常等於正確回答的題目數,或廣義地說,在測驗上獲得的分數。 |
真實分數 (True Score) | |
誤差分數 (Error Score) | 你觀測到的分數與你真實分數的差距。 |
良好的測驗須兼具有效性 (validity,效度) 與可靠性 (reliability,信度):
效度與信度 | 說明 |
有效性 (validity, 又稱效度) | 一把刻度很精確、不會熱脹冷縮,就是「信度」很高的尺,但如果用這把尺來量一群人的體重,就不適用,量測結果就不是很「有效」。 |
可靠性 (reliability, 又稱信度) | 有效性是一個測驗分數代表想要測量特徵的程度,譬如一把捲尺昨天量一個人的身高是 170 cm,今天再量卻變成 165 cm,一個人不可能一天差 5cm,顯然這把尺有問題 ,量測結果「信度」不 高。 |
confidence interval, CI:由樣本資料定義一段數值區間,宣稱有多少信心以估計母體的參數包含於此區間內。該數值區間上、下限稱為信賴界限 (confidence limit)。用以估計的信心程度稱為信賴(心)水準 (confidence level)。一般常以 95% 或 99% 為信賴水準指標;相對應的 Z分數(相差幾個標準差) 分別為 1.96 與 2.58。可表示為:
信賴水準 | 說明 |
95% 信心估計 母群體平均數 | |
99% 信心估計 母群體平均數 | |
【Hack #7】度量水平 (Measure Up):四種度量水平 (levels of measurement) 決定了再測量中所產生的分數可以如何被使用。如果你沒有正確的度量水平,你可能無法依照你想要的方式來把玩那些分數 (scores)。度量水平決定了哪種統計分析是恰當的、有意義的。度量 (measurement) 是依據某些有意一把數字指定給事物的活動,可以是實際存在的物體 (ex. 岩石),也可以是抽象的概念 (ex. 聰明才智)。度量水平有四種:名目 (nominal)、順序 (ordinal)、等距 (interval) 和等比 (ratio)
度量水平 | 說明 |
名目 (nominal) | 
|
順序 (ordinal) | 若你分析分數的方式是要來測表現作為某種順序或等級的證據,那就是用順序水平 (ordinal level) 來進行測量。 例如,教育程度包含小學、初中、高中、學士、碩士、博士等;服務評等包含傑出、好、欠佳。 你可以將分數相互比較,但對於分數間的距離一無所知。在賽跑中的前三名,第一名可能僅領先第二名 1 秒.,第二名可能比第三名快了 30 秒。
|
等距 (interval) | 在華氏溫度計上,70 與 69 度之間的有意義的差異,就是 1 度,等於 32 與 21 度之間的差異。那 1 度被假設是等量的熱,不管該間距 (interval) 出現在溫度計的哪裡。 等距水平提供的資訊較順序水平多,而且你可以對分數進行有意義的平均,大多數的教育和心理學測量都使用等距水平。 但是,我們不使用比值 (fractions) 或比率 (ratios) 來做比較,例如,討論溫度時,我們不會說今天 (40 度) 是昨天 ( 80 度) 的一半熱;討論 IQ 時,,我們不會說 A 生 (IQ 120) 比 B 生 (IQ 90) 多聰明 1/3。
|
等比 (ratio) | |
度量水平的區別:盡可能使用最高水平的測量,也就是等比 (ratio)
度量水平 | 強項 | 弱項 | 可運用算式 | 定性或定量 |
名目 (nominal) | 描述類別資料 | 數字不代表量值 | ﹦≠ | 定性,如性別 |
順序 (ordinal) | 允許分數間的比較 | 很難做出分數摘要 | ﹦≠ > < | 定性,如服務平等包含傑出、好、欠佳 |
等距 (interval) | 大多數統計分析都可行 | 無法進行比例式比較 | ﹦≠ > < + − | 定量,如溫度、緯度、年份等 |
等比 (ratio) | 真 0 (true zero) 允許我們進行所可能的統計分析 | 某些感興趣的變數沒有 true 0 | ﹦≠ > < + − ×÷ | 定量,如價格、年齡、高度、絕對溫度、絕大多數物理量 |
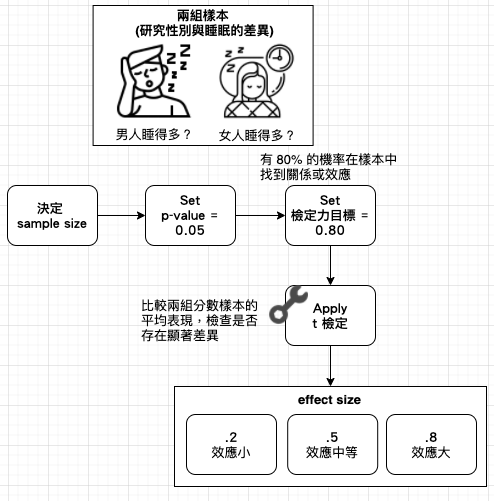
【Hack #8】提升檢定力 (Power Up):社會科學中的成功定義,通常就是找到具有統計顯著性的新發現。為了增加發現某些事情或任何東西的機率,精通統計學的超級科學家主要的目標都是增強統計檢定力 (power)。統計分析經常需要判斷在某個樣本中觀察到的一個特定的值是否是碰巧出現的,此過程稱為顯著性檢定 (test of significane)。顯著性檢定會產生機率值 (p-value, probability value),如果 p-value 很小,說明原假設情況的發生的概率很小,而如果出現了,根據小概率原理,我們就有理由拒絕原假設,p-value 越小,我們拒絕 H0 的理由越充分。在大家習慣採用 0.05 當作一個臨界,當研究的 p 值小於這個臨界值的時候就宣稱研究結果達到統計顯著,也就是說大家普遍同意接受 5%犯錯的可能性。
統計研究常見陷阱
陷阱 | 解法 |
從樣本自以為找到母體某項特性,但是只存在於樣本中 | 以對母體具有代表性的方式進行抽樣 (Hack #19) |
在樣本找不到任何特性,母體卻確實存在 | 增強統計檢定力 (power) |
檢定力並非找到顯著結果 (significant result) 的機率,它是某種關係「真的存在」時,找到該種關係的機率。檢定力的公式包含三個組成部分:
檢定力的公式包含三個組成部分 |
① 樣本大小 (sample size) |
② 要達到 (小於)預先決定的顯著性水平 (p-value) |
③ 效應大小 (effect size, 母體中該項關係的強度) |
Z 檢定 vs T 檢定
檢定 | 說明 |
Z 檢定 | 用於大樣本(樣本數大於30,統計學上可代表母體) |
T 檢定 | t 檢定則用於小樣本(樣本數小於30)。t 檢定的運算中包含自由度,當樣本數越高,自由度越高,其結果與 Z 檢定也越相近。 |
學生 t 檢定 (Student’s t-test) (https://reurl.cc/7yje0N)
t 檢定 | 說明 |
單一樣本 t 檢定 (one sample test) TTEST(範圍_1, 範圍_2, 尾數=2, 類型=2) | |
獨立樣本 t 檢定 (Independent sample t-test) TTEST(範圍_1, 範圍_2, 尾數=2, 類型=3) | 在進行獨立樣本t檢定之前,我們會先進行變異數的同質性檢定,若兩組資料的變異數具有同質性,我們便可使用 Student’s t-test;反之,若兩組資料的變異數不具同質性,我們則必須對 t檢定的自由度做修正,此時會改採修正版的Welch’s t-test 來進行檢驗。 獨立樣本 t 檢定常用來檢驗兩組相互獨立的資料之間是否有顯著差異 (例如:想要知道A、B兩班學生的生物成績是否有顯著差異)。進行檢驗前,我們希望確定每一組樣本平均數的確能夠被互相比較,因此兩組樣本除了需要符合常態分配外,也希望其離散分布的狀況能具有相似性,亦即,樣本的變異數需要具有同質性。 獨立資料:在機率論中,說明兩個事件獨立,是指在一次的實驗中某一事件的發生不會影響到另一件事情發生的機率,舉例來說:擲一枚公正的銅板時,出現「人頭」的事件與出現「數字」的事件不會互相影響,即為兩事件獨立。
|
成對樣本 t 檢定 (Paired samples t-test) TTEST(範圍_1, 範圍_2, 尾數=2, 類型=1) | 相較於獨立樣本 t 檢定之用來比較兩組「獨立樣本」間的平均數差異,成對樣本t檢定則是用來比較兩組「相依樣本」間的平均數差異。 舉例來說,當我們今天希望知道某種療程對於肝腫瘤大小是否有明顯作用時,我們就可以使用成對樣本 t 檢定來進行檢驗:首先,我們從肝腫瘤病患名冊中隨機挑選出一群病患來當作樣本,測量並記錄該群病患治療前的肝腫瘤大小;接著讓這群病患進行治療,待療程結束後再次測量並紀錄病患治療後的肝腫瘤大小。之後,使用成對樣本t檢定來檢驗療程前後的資料變化,若前後資料有顯著差異,我們便認為此療程對肝腫瘤的大小變化的確有影響;反之,則認為此療程對肝腫瘤的大小沒有明顯影響。
|
t 檢定範例
【單一樣本 t 檢定】 執行兩樣本具有同一變數 (同質性) 的檢定 |
| 【獨立樣本 t 檢定】 執行兩樣本不具有同一變數 (異質性) 的檢定 |
| 【成對樣本 t 檢定】 執行配對檢定
|
A 組學生體重 | B 組學生體重 |
| A 組學生體重 | B 組學生體重 |
| 原始體重 | 運動一個月後體重 |
64 | 57 |
| 64 | 49 |
| 70 | 72 |
67 | 64 |
| 67 | 39 |
| 87 | 91 |
66 | 53 |
| 66 | 58 |
| 84 | 84 |
61 | 52 |
| 61 | 53 |
| 76 | 79 |
52 | 53 |
| 52 | 71 |
| 67 | 69 |
62 | 54 |
| 62 | 53 |
| 66 | 69 |
63 | 56 |
| 63 | 54 |
| 83 | 84 |
61 | 60 |
| 61 | 68 |
| 46 | 48 |
53 | 61 |
| 53 | 60 |
| 71 | 71 |
58 | 58 |
| 58 | 52 |
| 88 | 90 |
單一樣本 t 檢定 | 0.0703 |
| 獨立樣本 t 檢定 | 0.1544 |
| 成對雙樣本 t 檢定 | 0.0012 |
T.TEST(A3:A12,B3:B12,2,2) |
| T.TEST(D3:D12,E3:E12,2,3) |
| T.TEST(G3:G12,H3:H12,2,1) |
p-value 是 0.0703,大於 0.05,表示兩群的學生體重並沒有明顯的不同 |
| p-value 是 0.1544,大於 0.05,沒有明顯證據顯示兩群學生的體重有差異 |
| p-value 是 0.001,遠小於 0.05,所以證明長期運動對於體重是有影響的。 |

Type I Error, Type II Error:α 與 β 互為拮抗,亦即 α 提高時、β 降低;反之亦然。統計學上認為犯 Type I Error 的後果相當嚴重 (i.e. 宣告無罪的人有罪),因此一般希望能將其發生的機率 (α) 控制在一定的程度 (0.05 or 0.01)。當固定 α 時,可透過增加樣本數達到降低 β 的目的。(http://shorturl.at/pqDOX)
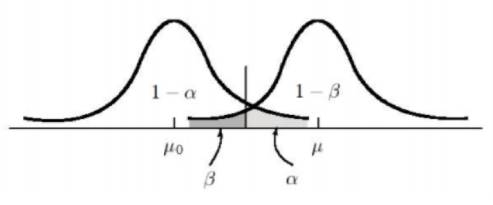
檢定錯誤 | 說明 |
Type I Error | |
Type II Error | |
在進行假說檢定時,p-value 也是一種幫助我們下決策的指標;p-value 的定義為: 在 H0(虛無假說)成立的情況下,檢定統計量的取樣分布中往 H1 方向超過或等於實際觀測到之檢定統計量值的尾端機率(下圖灰色部分)。p-value 可用來在任何顯著水準下作檢定,若 p-value ≤α 決策為棄卻 H0;若 p-value >α 決策為在 α 的顯著水準下,不棄卻 H0。 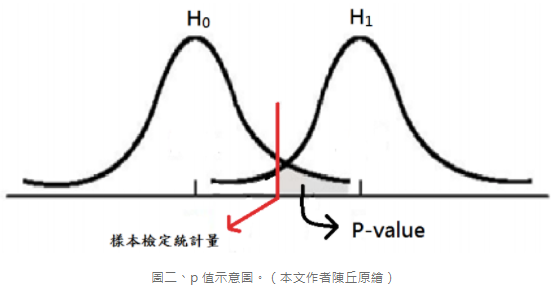
|
虛無假設 (H0) 必須是假的,否則你「發現」新知的機率相當渺茫。如果你「發現」某個東西,但實際不存在(拒絕一個真的虛無假設),你就犯了 Type I error。母體中你的研究變數間必須真的有關係存在,你才能在樣本資料中找到它。
檢定力不是成功機率,也不是達成某個顯著水平的機率。這是在「研究者估計的所有值最終都正確」的前提下,達到某個顯著水平的機率。
【Hack #9】顯示因果關係 (Show Cause and Effect):如果你希望展現的是某件事情導致另一件事,你必須遵循統計研究人員以建立的一些規則。群組設計 (group designs) 有四種基本類型,依據設計是否能為因果關係提供強烈的、中等的、微弱的、完全沒有的證據來分類:
group designs | 說明 |
非實驗設計 | |
前實驗設計 | |
準實驗設計 | |
實驗設計 | |
研究結果的有效性考量 (validity concerns):
有效性考量 | 有效性問題 |
統計結論有效性 (statistical conclusion validity) | 變數間有關係存在嗎? |
內部有效性 (internal validity) | 這個關係是一種因果關係嗎? |
建構有效性 (construct validity) | 這個因果關係存在於你相信應受影響的變數間嗎? |
外部有效性 (external validity) | 這因果關係到處都有且會影響到每個人嗎? |
在做因果主張 (casual claims) 和推廣結果主張 (claims of generalizability) 之有效性,常見的威脅:
推論有效性的威脅 | 說明 | 解法 |
歷程中同時存在的事件 (history) | 外在事件可能影響結果 | 使用一個「比較組」 (不熟藥物或干預或其他處理得比較組),並將受試者「隨機」指派到各組中。 |
成熟的效果 (maturation) | 研究過程,受試者自然也會知道測試方式,導致結果不準 | 「隨機」將參與者指派到實驗組和控制組 |
選擇性偏差 (selction) | 指派受試者到各組的方式可能有性統系偏差存在 | 「隨機」指派受試者 |
測驗的效果 (testing) | 單純只是接受 pretest 可能影響到研究變數的水平 | 「隨機」指派受試者到實驗組與比較組,並讓兩者都接受 pre-test。 |
測量工具的偏差 (instrumentation) | 測量過程中可能有系統性的偏差出現 | 使用有效的、標準化的、給分客觀的測驗 |
霍桑效應 (hawthorne effect) | 參與者意識到他們是研究中的受試者時,會影響測驗結果 | 讓受試者不清楚你預期的是什麼結果,或者進行雙盲研究 (double-blind study),讓受試者與研究人員都不知道他們所接受的處置 |
- 【Hack #10】識別出重大發現 (Know Big When You See It):你剛讀了一篇科學新發現,但是這樣的發現很重大嗎?具有統計顯著性 (statistically significant) 的發現 ≠ 重要或有用的發現。應用效應大小 (effect size) 來判斷其重要性。effect size 是一個標準化的值,用來表現兩個變數間某個關係的強度。例如,每天服用半顆 aspirin 來降低心臟病發的風險值得嗎?到底降低多少風險?
No comments:
Post a Comment